Исследование трехфазного асинхронного двигателя методом непосредственной нагрузки
В соответствии с принципом обратимости асинхронные машины могут работать в режиме генератора, двигателя и тормозном. Но основным является двигательный режим, поэтому изучение асинхронных машин дается на примере двигателя. Обратите внимание на сходство и различие в устройстве асинхронных двигателей (АД) с короткозамкнутым и фазным ротором.
Рабочий процесс АД очень схож с рабочим процессом трансформатора. Порядок построения векторной диаграммы АД такой же, как и трансформатора. О потерях в АД дает представление энергетическая диаграмма.
Особое внимание следует уделить вращающему моменту, который является важнейшей характеристикой АД. Величина вращающего момента значительно изменяется в зависимости от скольжения. Эта зависимость выражается механической характеристикой двигателя. При изучении механической характеристики нужно выделить участки устойчивой работы и усвоить математические зависимости для расчета механической характеристики. Значительный интерес представляет зависимость параметров (частота вращения, КПД, полезный момент, коэффициент мощности, ток, потребляемый из сети) от полезной мощности на валу двигателя. Эти зависимости называются рабочими характеристиками.
Асинхронные машины применяются на практике главным образом как двигатели. Наибольшее распространение имеют трехфазные асинхронные двигатели. Они находят себе самое широкое применение на заводах, фабриках, в сельском хозяйстве, на строительных работах, для вспомогательных механизмов электрических станций. Особенно много требуется трехфазных двигателей мощностью от 0,4 до 100 кВт. Такие двигатели массового применения электромашиностроительными заводами выпускаются ежегодно на миллионы киловатт. Большое количество двигателей выпускается также на мощности свыше 100 кВт.
Однофазные асинхронные двигатели в настоящее время выполняются, как правило, в виде малых машин обычно на мощности не свыше 0,5 кВт.
Обмотки статора и ротора асинхронных машин между собой электрически не связаны; между ними существует только магнитная (трансформаторная) связь, называемая также индуктивной, что дало повод назвать асинхронные машины индукционными. Однако это название в Советском Союзе почти не применяется.
Обмотка статора обычно является первичной обмоткой при работе машины двигателем, так как к ней в этом случае подводится электрическая энергия. Токи обмотки статора совместно с токами обмотки ротора создают в двигателе вращающееся магнитное поле. Обмотка ротора при этом служит в качестве вторичной. Токи, наведенные в ней вращающимся полем, взаимодействуя с ним, создают электромагнитные силы, заставляющие ротор вращаться.
Асинхронные двигатели выполняются или с короткозамкнутой обмоткой на роторе, или с обмоткой на роторе (обычно трехфазной), соединенной с контактными кольцами. В соответствии с этим различают короткозамкнутые двигатели и двигатели с контактными кольцами. Последние условие называются также двигателями с фазным ротором.
На щитке асинхронного двигателя указываются следующие номинальные величины его:
1) мощность (на валу), кВт или Вт;
2) линейное напряжение обмотки статора, В;
3) линейный ток, А;
4) частота тока, Гц;
5) частота вращения ротора (число оборотов в минуту);
6) коэффициент полезного действия;
7) коэффициент мощности (косинус угла сдвига фаз между напряжением и током фазы обмотки статора);
8) напряжение на контактных кольцах (при неподвижном роторе) и ток обмотки ротора (при номинальном режиме) для двигателя с контактными кольцами.
Кроме того, на щитке указываются схема соединений обмотки статора, режим работы (продолжительный, кратковременный или повторно-кратковременный), для которого предназначен двигатель, и полный вес его в килограммах.
Электромагнитный момент асинхронного двигателя создается взаимодействием тока в обмотке ротора с вращающимся магнитным полем. Электромагнитный момент М пропорционален электромагнитной мощности:
М = Рэм /ω1 ,
где ω1 = 2 π n1 /60 = 2π f1 – угловая синхронная скорость вращения.
Подставив в выражение значение электромагнитной мощности, получим
М = Рэ2/ (ω1 s) = m1 I ′ 22 r′2 /(ω1 s),
т. е. электромагнитный момент асинхронного двигателя пропорционален мощности электрических потерь в обмотке ротора.
Подставив значение тока ротора, получим формулу электромагнитного момента асинхронной машины (Н·м):
М = 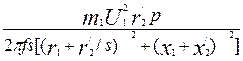 .
.
Параметры схемы замещения асинхронной машины r1, r '2 , х1 и х'2 , входящие в выражение, являются постоянными, так как их значения при изменениях нагрузки машины остается практически неизменными. Также постоянными можно считать напряжение на обмотке фазы статора U1 и частоту f1. В выражении момента M единственная переменная величина – скольжение s, которое для различных режимов работы асинхронной машины может принимать разные значения в диапазоне от + ∞ до – ∞.
Рассмотрим зависимость момента от скольжения M = f (s) при U1 = const, f1 = const и постоянных параметрах схемы замещения. Эту зависимость принято называть механической характеристикой асинхронной машины. Анализ выражения, представляющего собой аналитическое выражение механической характеристики M = f (s), показывает, что при значениях скольжения s = 0 и s = ∞ электромагнитный момент М = 0. Из этого следует, что механическая характеристика M = f (s) имеет максимум.
Для определения величины критического скольжения sкр, соответствующего максимальному моменту, необходимо взять первую производную от выражения и приравнять ее нулю: dM /ds = 0. В результате
sкр = ± r/2 / 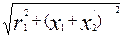 .
.
Подставив значение критического скольжения в выражение электромагнитного момента, после ряда преобразований получим выражение максимального момента (Н·м):
Mmax = ± 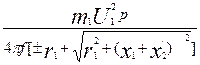 .
.
Знак плюс соответствует двигательному, а знак минус — генераторному режиму работы асинхронной машины.
Для асинхронных машин общего назначения активное сопротивление обмотки статора r1 намного меньше суммы индуктивных сопротивлений: r1 << (x1 +х'2). Поэтому, пренебрегая величиной r1, получим упрощенные выражения критического скольжения
Sкр ≈ ± r/2 /(x1 +x/2)
и максимального момента (Н·м)
Mmax = ± 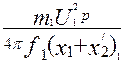 .
.
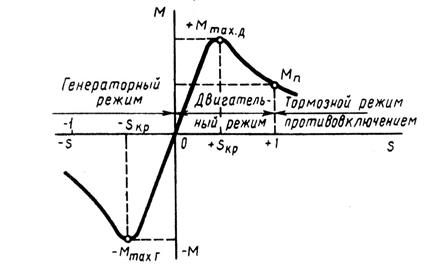
Рисунок 19 – Зависимость режимов работы
асинхронной машины от скольжения
Анализ выражения показывает, что максимальный момент асинхронной машины в генераторном режиме больше, чем в двигательном (Mmax г > Мmах д). На рисунке 19 показана механическая характеристика асинхронной машины М = f (s) при U1 = const. На этой характеристике указаны зоны, соответствующие различным режимам работы: двигательный режим (0 < s ≤ 1), когда электромагнитный момент М является вращающим; генераторный режим ( - ∞ < s < 0) и тормозной режим противовключением (1 < s < + ∞), когда электромагнитный момент М является тормозящим.
Электромагнитный момент асинхронного двигателя пропорционален квадрату напряжения сети: M ≡ U12. Это в значительной степени отражается на эксплуатационных свойствах двигателя: даже небольшое снижение напряжения сети вызывает заметное уменьшение вращающего момента асинхронного двигателя. Например, при уменьшении напряжения на 10% относительно номинального (U1 = 0,9Uном) электромагнитный момент двигателя уменьшается на 19%: M/ =0,92 M, где М – момент при номинальном напряжении сети, а М/ – момент при пониженном напряжении.
Для анализа работы асинхронного двигателя удобнее воспользоваться механической характеристикой M = f (s), представленной на рисунке 20. При включении двигателя в сеть магнитное поле статора, не обладая инерцией, сразу же начинает вращение с синхронной частотой n1, в то же время ротор двигателя под влиянием сил инерции в начальный момент пуска остается неподвижным (n2 = 0) и скольжение s = 1.
Подставив скольжение s = 1, получим выражение пускового момента асинхронного двигателя (Н·м):
Мп = 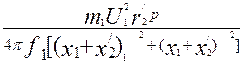
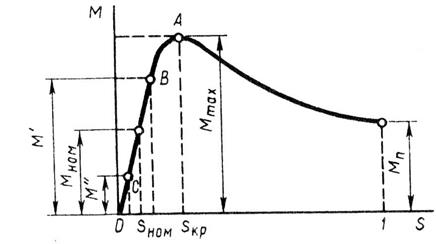
Рисунок 20 – Зависимость электромагнитного момента
асинхронного двигателя от скольжения
Под действием этого момента начинается вращение ротора двигателя, при этом скольжение уменьшается, а вращающий момент возрастает в соответствии с характеристикой М = f (s). При критическом скольжении sкр момент достигает максимального значения Мmах. С дальнейшим нарастанием частоты вращения (уменьшением скольжения) момент М начинает убывать, пока не достигнет установившегося значения, равного сумме противодействующих моментов, приложенных к ротору двигателя: момента х.х. M0 и полезного нагрузочного момента (момента на валу двигателя) М2, т. е.
М = М0 + M2 = Mст .
Следует иметь в виду, что при скольжениях, близких к единице (пусковой режим двигателя), параметры схемы замещения асинхронного двигателя заметно изменяют свои значения. Объясняется это в основном двумя факторами: усилением магнитного насыщения зубцовых слоев статора и ротора, что ведет к уменьшению индуктивных сопротивлений рассеяния x1 и х'2, и эффектом вытеснения тока в стержнях ротора, что ведет к увеличению активного сопротивления обмотки ротора r/2. Поэтому параметры схемы замещения асинхронного двигателя, используемые при расчете электромагнитного момента, не мoгyт быть использованы для расчета пускового момента.
Статический момент Мст равен сумме противодействующих моментов при равномерном вращении ротора (n2 = const). Допустим, что противодействующий момент на валу двигателя М2 соответствует номинальной нагрузке двигателя. В этом случае устано вившийся режим работы двигателя определится точкой на механической характеристике с координатами М = Мном и s = sном, где Мном и shom — номинальные значения электромагнитного момента и скольжения.
Из анализа механической характеристики также следует, что устойчивая работа асинхронного двигателя возможна при скольжениях меньше критического (s < sкр), т. е. на участке ОА механической характеристики. Дело в том, что именно на этом участке изменение нагрузки на валу двигателя сопровождается соответствующим изменением электромагнитного момента. Так, если двигатель работал в номинальном рехиме (Мном; shom), то имело место равенство моментов: Мном = M0 + М/2. Если произошло увеличение нагрузочного момента M2 до значения М'2, то равенство моментов нарушится, т. е. Мном < М0 + М'2, и частота вращения ротора начнет убывать (скольжение будет увеличиваться). Это приведет к росту электромагнитного момента до значения M' = М0 + М'2 (точка B), после чего режим работы двигателя вновь станет установившимся. Если же при работе двигателя в номинальном режиме произойдет уменьшение нагрузочного момента до значения М"2 то равенство моментов вновь нарушится, по теперь вращающий момент окажется больше суммы противодествующих: Мном > М0 + М″2 . Частота вращения ротора начнет возрастать (скольжение будет уменьшаться), и это приведет к уменьшению электромагнитного момента М до значения М" = М0 + М″2 (точка С); устойчивый режим работы будет вновь восстановлен, но уже при других значениях М и s.
Работа асинхронного двигателя становится неустойчивой при скольжениях s ≥ sкр. Так, если электромагнитный момент двигателя М = Мmах, а скольжение s = sкp, то даже незначительное увеличение нагрузочного момента М2, вызвав увеличение скольжения s,приведет к уменьшению электромагнитного момента М. За этим следует дальнейшее увеличение скольжения и т. д., пока скольжение не достигнет значения s = 1, т. е. пока ротор двигателя не остановится.
Таким образом, при достижении электромагнитным моментом максимального значения наступает предел устойчивой работы асинхронного двигателя. Следовательно, для устойчивой работы двигателя необходимо, чтобы сумма нагрузочных моментов, действующих на ротор, была меньше максимального момента Мст = (М0 + М2) < Мmах. Но чтобы работа асинхронного двигателя была надежной и чтобы случайные кратковременные нагрузки не вызывали остановок двигателя, необходимо, чтобы он обладал перегрузочной способностью. Перегрузочная способность двигателя λ определяется отношением максимального момента Мmax к номинальному Мном. Для асинхронных двигателей общего назначения перегрузочная способность составляет λ = Mmax /Mном = 1,7 ÷ 2,5.
Следует также обратить внимание на то, что работа двигателя при скольжении s < sкр т. е. на рабочем участке механической характеристики, является наиболее экономичной, так как она соответствует малым значениям скольжения, а следовательно, и меньшим значениям электрических потерь в обмотке ротора Рэ2 = s Pэм.
Пример 1. Рассчитать данные и построить механическую характеристику М 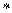 = f (s) трехфазного асинхронного двигателя с короткозамкнутым ротором типа 4А160М4УЗ номинальной мощностью 18,5 кВт, напряжением 220/380 В, частотой вращения 1465 об/мин. Параметры схемы замещения этого двигателя: r1 = 0,263 Ом, x1 = 0,521 Ом, r/2 = 0,158 Ом, х/2 = 0,892 Ом. Перегрузочная способность двигателя λ = 2,3, кратность пускового момента Мп /Мном = 1,0.
= f (s) трехфазного асинхронного двигателя с короткозамкнутым ротором типа 4А160М4УЗ номинальной мощностью 18,5 кВт, напряжением 220/380 В, частотой вращения 1465 об/мин. Параметры схемы замещения этого двигателя: r1 = 0,263 Ом, x1 = 0,521 Ом, r/2 = 0,158 Ом, х/2 = 0,892 Ом. Перегрузочная способность двигателя λ = 2,3, кратность пускового момента Мп /Мном = 1,0.
Решение. Для получения данных, необходимых для построения механической характеристики двигателя, определяем номинальный электромагнитный Мном пусковой Мп и максимальный Мmax моменты, а также два промежуточных значения момента при скольжениях s > sкр.
Номинальное скольжение по (10.1) sном = (1500 - 1465)/ 1500 = 0,023 .
Номинальный электромагнитный момент
Мном = 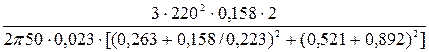 =121 Н·м.
=121 Н·м.
Пусковой момент двигателя Мп = Мном = 121 Н·м.
Максимальный момент двигателя Мmax = λМном = 2,3·121 = 278 Н·м.
Критическое скольжение sкр = 0,158/ (0,521 + 0,892) = 0,112 .
Электромагнитные моменты при скольжениях s = 0,2, s = 0,4 и s = 0,7:
М0,2 = 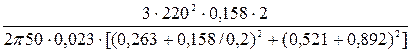 =236 Н·м.
=236 Н·м.
М0,4 = 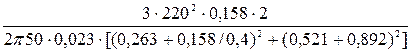 =150 Н·м.
=150 Н·м.
М0,7 = 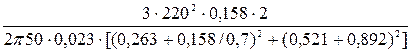 =93,6 Н·м.
=93,6 Н·м.
Таблица 9 – Результаты вычислений
| S | 0,023 | 0,112 | 0,20 | 0,4 | 0,7 | 1,0 | |
| M, Н·м | 93,6 | ||||||
М 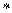 =М/ Mmax =М/ Mmax
| 0,44 | 1,0 | 0,85 | 0,54 | 0,34 | 0,44 |
Механическая характеристика M 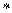 = f (s), построенная по этим данным, приведена на рисунке 21.
= f (s), построенная по этим данным, приведена на рисунке 21.
Применение приведенной выше формулы для расчета механических характеристик асинхронных двигателей не всегда возможно, так как параметры схемы замещения двигателей обычно не приводятся в каталогах и справочниках, поэтому для практических расчетов обычно пользуются упрощенной формулой момента. В основу этой формулы положено допущение, что активное сопротивление обмотки статора асинхронного двигателя r1 = 0, при этом
M = Mmax 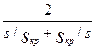 .
.
Критическое скольжение определяют по формуле
sкр = sном (λ + 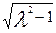 ) .
) .
Расчет механической характеристики намного упрощается, если его вести в относительных единицах M 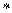 = M/ Mном. В этом случае уравнение механической характеристики имеет вид
= M/ Mном. В этом случае уравнение механической характеристики имеет вид
M 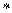 =
= 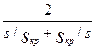 .
.
Пример 2. Рассчитать механическую характеристику трехфазного асинхронного двигателя типа 4А160М4УЗ (18,5 кВт, 1465 об/мин, λ = 2,3, Mп/ Mном = 1,0) в относительных единицах M 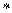 = f (s) по упрощенной формуле и полученные результаты сравнить с данными, рассчитанными в примере 1.
= f (s) по упрощенной формуле и полученные результаты сравнить с данными, рассчитанными в примере 1.
Решение. Критическое скольжение
sкр = 0,023 (2,3 + 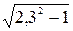 ) = 0,100 .
) = 0,100 .
Относительное значение момента M 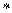 при скольжениях:
при скольжениях:
sном = 0,023 ; sкp = 0,100;
s = 0,2; s = 0,4 s = 0,7;
M 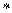 ном =
ном = 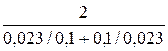 = 0,46;
= 0,46;
M 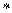 =
= 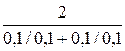 =1;
=1;
M 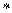 0,2 =
0,2 = 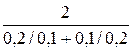 = 0,80;
= 0,80;
M 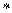 0,4 =
0,4 = 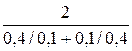 = 0,47;
= 0,47;
M 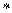 0,7 =
0,7 = 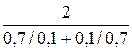 =0,28.
=0,28.
Таблица 10 – Результаты расчета
| S | 0,023 | 0,1 | 0,2 | 0,4 | 0,7 |
М 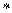
| 0,046 | 1,0 | 0,80 | 0,47 | 0,28 |
| Ошибка,% по сравнению с расчетом примера 13.2 | -4,3 | — | +5,9 | -6,8 | +16,6 |
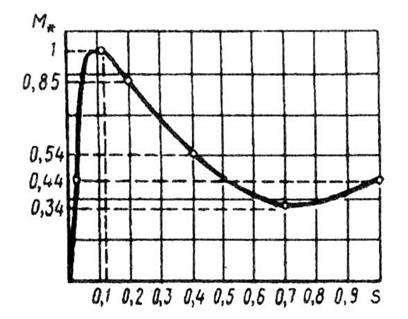
Рисунок 21 – Механическая характеристика
асинхронного двигателя типа 4А160М4УЗ
Применение упрощенной формулы наиболее целесообразно при расчете рабочего участка механической характеристики и при скольжениях s < sкр,так как в этом случае величина ошибки не превышает значений, допустимых для технических расчетов. При скольжениях s > sкрошибка может достигать 15-17%. Это подтверждается расчетами примера 2.
Рабочие характеристики асинхронного двигателя (рисунок 22) представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.
Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя
n2 = n1(1 - s).
Скольжение
s = Pэ2/ Pэм ,
т. е. скольжение двигателя, а, следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности Рэм. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1. По мере увеличения нагрузки на валу
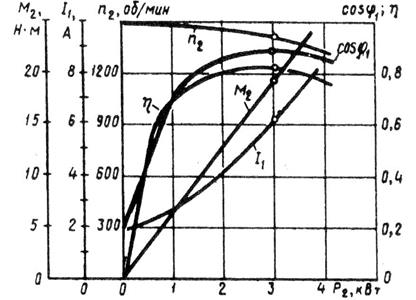
Рисунок 22 – Рабочие характеристики асинхронного двигателя
двигателя отношение мощностей растет, достигая значений 0,01—0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора r2' угол наклона этой кривой увеличивается. В этом случае изменения частоты вращения n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2' возрастают электрические потери в роторе.
Зависимость М2 =f(P2). Зависимость полезного момента на валу двигателя М2 от полезной мощности Р2 определяется выражением
M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2,
где Р2 – полезная мощность, Вт;
ω2 = 2πf 2/ 60 – угловая частота вращения ротора.
Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.
Рисунок 23 – Векторная диаграмма асинхронного
двигателя при небольшой нагрузке
Зависимость cosφ1 = f (P2). В связи с тем что ток статора I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму х.х. Объясняется это тем, что ток х.х. I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора 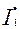 , относительно напряжения
, относительно напряжения 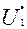 , получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рисунок 23). Коэффициент мощности асинхронных двигателей в режиме х.х. обычно не превышает 0,2. При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80-0,90) при нагрузке, близкой к номинальной. Дальнейшее увелиичение нагрузки сопровождается уменьшением cosφ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе. В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cosφ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в
, получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рисунок 23). Коэффициент мощности асинхронных двигателей в режиме х.х. обычно не превышает 0,2. При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80-0,90) при нагрузке, близкой к номинальной. Дальнейшее увелиичение нагрузки сопровождается уменьшением cosφ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе. В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cosφ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в 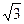 раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в
раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в 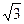 раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя. На рисунке 24 представлены графики зависимости cosφ1, асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).
раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя. На рисунке 24 представлены графики зависимости cosφ1, асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).
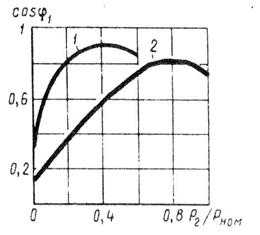
Рисунок 24 – Зависимость cos φ1 от нагрузки при
соединении обмотки статора звездой (1) и треугольником (2)
Дата добавления: 2015-10-13; просмотров: 7407;
