Моделирование очереди

Таким образом, при данных случайных наборах чисел в колонках A и В и покупателям приходилось стоять в очереди (колонка G), и продавцу - в ожидании покупателя (колонка H).

При моделировании систем такого вида возникают следующие вопросы. Какое среднее время приходится стоять в очереди к прилавку? Чтобы ответить на него, следует найти

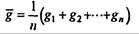
в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Конечно, эти выборочные средние сами по себе - случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки, не слишком отличающиеся друг от друга). Доверительные интервалы, в которых находятся точные средние значения (т.е. математические ожидания соответствующих случайных величин) при заданных доверительных вероятностях находятся методами математической статистики.

Сложнее ответить на вопрос, каково распределение случайных величин G и Н при заданных распределениях случайных величин А и В. Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин A и В - скажем, для А в диапазоне от 0 до 10 минут и В - от 0 до 5 минут. Для построения методом статистических испытаний распределений величин G и Н поступим так: найдем в достаточно длинной серии испытаний (реально - в десятках тысяч, что на компьютере делается достаточно быстро) значения g_max (для Н все делается аналогично) и разделим промежуток [0, g_max] на т равных частей - скажем, вначале на 10 - так, чтобы в каждую часть попало много значений g_i. Разделив число попаданий n_k в каждую из частей на общее число испытаний n, получим набор чисел p_k = 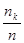(k = 1, 2,...,n). Построенныепо ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии.

Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше т минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой х = т и у = 0, к площади всей фигуры.

Следующая программа позволяет моделировать описанный выше процесс. На выходе она дает средние значения и дисперсии случайных величин g и h, полученные по выборке, максимальный объем которой порядка 10000 (ограничение связано с малой допустимой длиной массива в PASCALe; чтобы его смягчить, использовано динамическое описание массивов g и h). Кроме того, программа строит гистограммы распределений величин g и h.

Программа 152. Моделирование очереди

Program Cohered;

(входной поток равновероятных событий;

динамические массивы позволяют значительно увеличить объем выборки)

Uses Crt, Graph;

Const N = 10000 (число членов выборки);

W1 = 10 (диапазон времен прихода от 0 дo wl};

W2 = 5 (диапазон времен обслуживания от 0 до w2};

Type Т = Array(l..N] Of Real; U = ^Т;

Var A, B, C, D, E, F, Aa, Bb, Cc, Dd, Ее, Ff, Dg, Dh, M : Real;

Sl, S2 : Double; I, K, J, I1, I2 : Integer;

LI, L2, V : Array [1..11] Of Real; G, H : U; Ch : Char;

Begin

If MaxAvail >= SizeOf(G) Then New(G);

If MaxAvail >= SizeOf(H) Then New(H);

Randomize; (ниже - имитационное моделирование)

Aa := 0; Bb := W2 * Random; Cc := 0; Ее := Bb; Ff := Bb;

G^[l] = 0; H^[1] := 0;

For К = 1 To 11 Do

Begin L1(K] := 0; L2[K] := 0 End;

For I = 2 To N Do

Begin

A := Wl * Random; В := W2 * Random;

С := Cc + A; If С > Ее Then D := С Else D := Ее;

E := D + B; F := E - C; G^[I] := F - B; H^[I] := D - Ее;

Cc := С; Ее := E;

If G^[I] <= 1 Then Ll[l] := Ll[l] + 1; If H^[1] = 0 Then

L2[l] := L2[l] + 1;

For К := 2 To 10 Do

Begin

If (G^[I] > К - 1) And (G^[I] <= K) Then L1[K] := L1[K] + 1;

If (H^[I] > K - 1) And (H^[I] <= K) Then L2[K] := L2[K] + 1;

End;

If G^[I] > 10 Then Ll[l1] := Ll[ll] + 1;

If H^[I] > 10 Then L2[ll] := L2[ll] + 1;

Sl := Sl + G^[l]; S2 := S2 + H^[I];

End;

For I := 1 To 11 Do (ниже - нормировка распределений g и h}

Begin

L1[I] := L1[I] / N; L2[I] := L2[I] / N

End;

(ниже - расчет средних и дисперсий величин g и h}

Sl := Sl / N; S2 := S2 / N; Dg := 0; Dh := 0;

For I := 1 То N Do

Begin

Dg := Dg + Sqr(G^[I] - Sl); Dh := Dh + Sqr(H^[I] - S2)

End;

Dg := Dg / N; Dh := Dh / N;

WriteLn('распределение величины g распределение величины h');

WriteLn;

For K := 1 To 11 Do

WriteLn ('11[', K, ']=', L1[K] : 6 : 4, '' : 20, '12(', К, ']=',

L2[K] : 6 : 4);

WriteLn;

WriteLn('выборочное среднее величины g=', S1 : 6 : 3,

' выборочная дисперсия величины g=', Dg : 6 : 3);

WriteLn('выборочное среднее величины h=', S2 : 6 : 3,

' выборочная дисперсия величины h=', Dh : 6 : 3);

Dispose(G); Dispose(H); WriteLn;

WriteLn('для продолжения нажать любую клавишу');

Repeat Until KeyPressed; Ch := ReadKey;

(ниже - построение гистограмм распределений величин g и h)

DetectGraph(I, К); InitGraph(I, К, '');

I := GetMaxX; К := GetMaxY; J := I Div 2; M :'= Ll[l];

For I1 := 2 То 11 Do If L1[I1] > M Then M := L1[I1];

For I1 := 1 To 11 Do V[I1] := L1[I1] / M;

Line(10, К - 10, J - 20, К - 10); Line[l0, К - 10, 10, 5) ;

OutTextXY(20, 100, 'распределение величины g');

For I1 := 1 To 11 Do

Begin

I2 := Round((K - 20) * (1 - V[I1])) + 10;

Line(I1 * 20 - 10, I2, I1 * 20 + 10, I2);

Line(I1 * 20 - 10, I2, I1 * 20 - 10, К - 10);

Line(I1 * 20 + 10, I2, I1 * 20 + 10, К - 10);

End;

Line(J + 20, К - 10, I - 10, К - 10);

Line(J + 20, К - 10, J + 20, 5) ;

OutTextXY(J + 30, 100, 'распределение величины h'); M := L2[l];

For I1 := 2 To 11 Do If L2[I1] > M Then M := L2[I1];

For I1 := 1 To 11 Do V[I1] := L2[I1] / M;

For I1 := 1 To 11 Do

Begin

I2 := Round((K - 20) * (1 - V[I1])) + 10;

Line(J + I1 * 20, I2, J + I1 * 20 + 20, I2);

Line(J + I1 * 20, I2, J + I1 * 20, К - 10);

Line(J + I1 * 20 + 20, I2, J + I1 * 20 + 20, К - 10);

End;

OutTextXY(200, GetMaxY - 10, 'для выхода нажать любую клавишу');

Repeat Until KeyPressed; CloseCraph

End.

Приведем для сравнения результаты расчета средних значений величин g, h и соответствующих среднеквадратичных отклонений Sg, Sh, полученные при одинаковых значениях всех параметров в пяти разных сериях испытании по 10000 событий в серии (табл. 7.9) (входной поток покупателей - процесс равновероятных событий с максимальным временем между приходами 10 мин, длительность обслуживания также распределена равновероятным образом в интервале от 0 до 5мин).

Таблица 7.9