Связь поверхностных интегралов первого и второго рода
Поверхностные интегралы первого и второго рода связаны друг с другом соотношением:
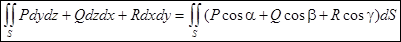
В этой формуле cosa, cosb, cosg - направляющие косинусы нормали к поверхности S в выбранную сторону поверхности.
12.14 Формула Гаусса–Остроградского
Формула Гаусса–Остроградского является аналогом формулы Грина–Остроградского. Эта формула связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью. Для вывода формулы Гаусса–Остроградского надо воспользоваться рассуждениями, подобными тем, которые использовались при нахождении формулы Грина–Остроградского.
Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум доугим координатным осям.
После этого полученные результаты обобщаются, приводя к формуле Гаусса–Остроградского:
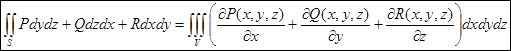
Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.
На практике формулу Гаусса – Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.
Тиеют место формулы:
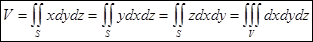
Пример. Найти формулу вычисления объема шара.
В поперечных сечениях шара (сечения параллельны плоскости XOY) получаются окружности. Уравнение шара имеет вид: 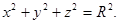
Найти объем шара можно по формуле:
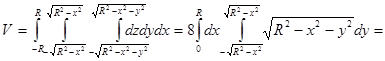
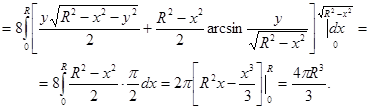
Для решения этой же задачи можно воспользоваться преобразованием интеграла к сферическим координатам. Это значительно упростит интегрирование.
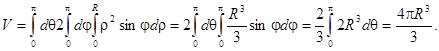
Дата добавления: 2015-10-13; просмотров: 2485;
