Свойства криволинейного интеграла второго рода
1) Криволинейный интеграл при перемене направления кривой меняет знак.

2) 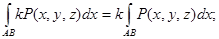
3) 
4) 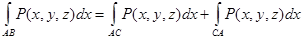
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.
6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то
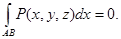
Аналогичные соотношения справедливы при интегрировании по у и z.
Теорема. Если кривая АВ – кусочно- гладкая, а функции P(x, y, z), Q(x, y, z) и
R(x, y, z) – непрерывны на кривой АВ, то криволинейные интегралы
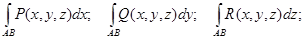
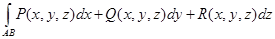
существуют.
Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:
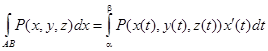
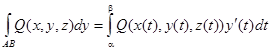
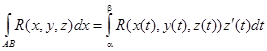
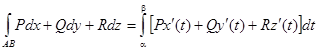
В случае, если АВ – плоская кривая, заданная уравнением y = f(x), то
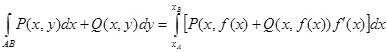
Пример. Вычислить криволинейный интеграл 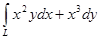 . L – контур, ограниченный параболами
. L – контур, ограниченный параболами 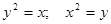 . Направление обхода контура положительное.
. Направление обхода контура положительное.


Представим замкнутый контур L как сумму двух дуг L1 = x2 и 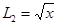

12.9 Формула Остроградского–Грина
Остроградский Михаил Васильевич (1861–1862) — русский математик.
Джордж Грин (1793–1841) — английский математик.
Иногда эту формулу называют формулой Грина, однако, Дж. Грин предложил в 1828 году только частный случай формулы.
Формула Остроградского–Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.
Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
 y
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
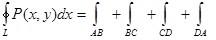
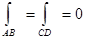
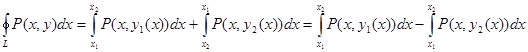

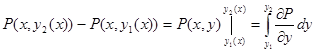
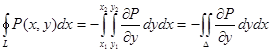
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:
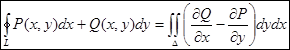
Эта формула называется формулой Остроградского–Грина.
Формула Остроградского –Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область D все время оставалась по левую сторону линии обхода.
Пример. Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.
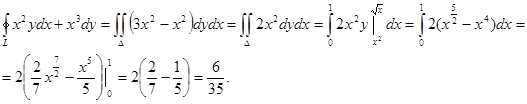
Формула Остроградского –Грина позволяет значительно упростить вычисление криволинейного интеграла.
Криволинейный интеграл не зависит от формы пути, если он вдоль всех путей, соединяющих начальную и конечную точку, имеет одну и ту же величину.
Условием независимости криволинейного интеграла от формы пути равносильно равенству нулю этого интеграла по любому замкнутому контуру, содержащему начальную и конечную точки.
Это условие будет выполняться, если подынтегральное выражение является полным дифференциалом некоторой функции, т.е. выполняется условие тотальности.
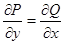
Дата добавления: 2015-10-13; просмотров: 957;
