Свойства криволинейного интеграла первого рода

1) Значение криволинейного интеграла по длине дуги не зависит от направления кривой АВ.

2) Постоянный множитель можно выносить за знак криволинейного интеграла.

3) Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций.

4) Если кривая АВ разбита на дуга АС и СВ, то

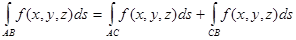
5) Если в точках кривой АВ , то

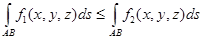
6) Справедливо неравенство:

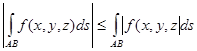
7) Если f(x, y, z) = 1, то

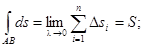
S — длина дуги кривой, l — наибольшая из всех частичных дуг, на которые разбивается дуга АВ.

8) Теорема о среднем.

Если функция f(x, y, z) непрерывна на кривой АВ, то на этой кривой существует точка (x₁, y₁, z₁) такая, что

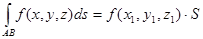
Для вычисления криволинейного интеграла по длине дуги надо определить его связь с обыкновенным определенным интегралом.

Пусть кривая АВ задана параметрически уравнениями x = x(t), y = y(t), z = z(t),

a £ t £ b, где функции х, у, z – непрерывно дифференцируемые функции параметра t, причем точке А соответствует t = a, а точке В соответствует t = b. Функция f(x, y, z) – непрерывна на всей кривой АВ.

Для любой точки М(х, у, z) кривой длина дуги АМ вычисляется по формуле

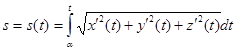
Длина всей кривой АВ равна:

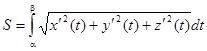
Криволинейный интеграл по длине дуги АВ будет находиться по формуле:

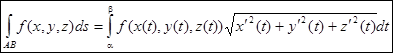
Таким образом, для вычисления криволинейного интеграла первого рода (по длине дуги АВ) надо, используя параметрическое уравнение кривой выразить подынтегральную функцию через параметр t, заменить ds дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.

Пример. Вычислить интеграл 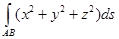по одному витку винтовой линии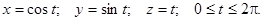

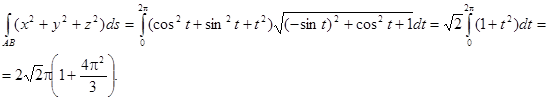
Если интегрирование производится по длине плоской кривой, заданной уравнением 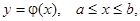то получаем: