Ошибки выборочного наблюдения. Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака происходит из-за ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими. Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения практически определить очень сложно, а иногда и невозможно, поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появление такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появление таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки является теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностями (~ —), которое не превышает ±. Предельной ошибкой выборки принято считать максимально возможное расхождение (~ —), т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П.Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле

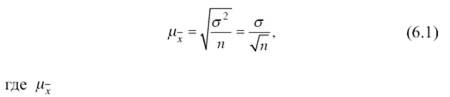
– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле

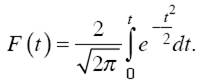
В математической статистике употребляют коэффициент доверия t, значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности (табл. 1).

Таблица 1 Коэффициент доверия t и соответствующие уровни доверительной вероятности

Коэффициент доверия позволяет вычислить предельную ошибку выборки,

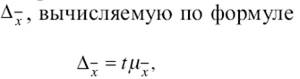
т. е. предельная ошибка выборки равна t-кратному числу средних ошибок выборки.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью. Как видно из последней графы табл. 1, вероятность появления ошибки равной или большей утроенной средней ошибки выборки, т. е.

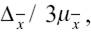
крайне мала и равна 0,003(1–0,997). Такие маловероятные события считаются практически невозможными, а потому величину

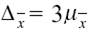
можно принять за предел возможной ошибки выборки.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней, которая показывает (с определенной вероятностью), насколько выборочная величина может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

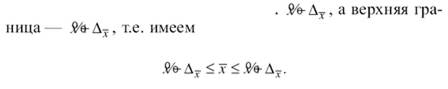
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

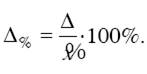
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.