Построение аксонометрических проекций предметов призматической и пирамидальной формы.

Построение аксонометрических проекций начинают с изображения основания или характерной грани предмета, то есть плоских фигур, расположенных в одной из плоскостей: фронтальной, горизонтальной или профильной. Поэтому рассмотрим сначала изображение плоских фигур.

Пример 1. Построение аксонометрических проекций равностороннего треугольника (рис. 3.44 и рис. 3.45).

1) Треугольник расположен во фронтальной плоскости. По оси х' откладывают по обе стороны от точки 0', принадлежащей оси z', отрезки b/2, равные в сумме d — стороне треугольника, а по оси z' — его высоту h. Полученные точки соединяют отрезками прямых.

2) Треугольник расположен в горизонтальной плоскости. По оси х' откладывают от точки 0', принадлежащей оси z отрезки b/2, равные в сумме b— стороне треугольника, а по оси у' — высоту h для изометрической (рис. 3.44) проекции и половину его высоты (h/2) — для фронтальной диметрической (рис. 3.45).

3) Треугольник расположен в профильной плоскости. По оси у откладывают половину стороны (b/2) для фронтальной диметрической проекции и сторону b для изометрической, а по оси z' — его высоту h.

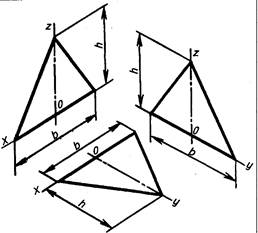
Рис. 3.44

Изображение равнобедренного треугольника в прямоугольной изометрической проекции

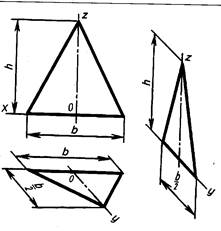
Рис.3.45

Изображение равнобедренного треугольника во фронтальной диметрической проекции

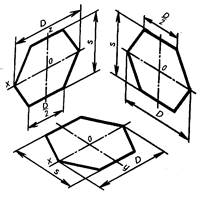
Рис. 3.46.

Изображение правильного шестиугольника в изометрической проекции

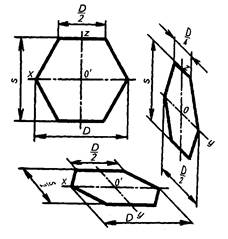
Рис. 3.47.

Изображение правильного шестиугольника во фронтальной диметрической проекции

Пример 2. Построение аксонометрических проекций правильного шестиугольника (рис. 3.46 и рис. 3.47).

1) Шестиугольник расположен во фронтальной плоскости. По оси х' симметрично точке 0' откладывают радиусы описанной окружности (d/2), равные размеру стороны шестиугольника, а по оси z, также симметрично точке 0 — отрезки S/2, равные половине расстояния между противоположными сторонами шестиугольника (их можно определить по формуле S = 0,866 В).

Через точки, полученные на оси z', проводят прямые, параллельные оси х, и симметрично оси z' откладывают на них отрезки, равные половине стороны шестиугольника (D/2). Полученные шесть точек соединяют отрезками прямых.

2) Шестиугольник расположен в горизонтальной плоскости. Построение выполняют, как было рассмотрено выше, с той лишь разницей, что расстояние S между противоположными сторонами (для фронтальной диметрической проекции S(2)) откладывают по оси у'.

3) Шестиугольник расположен в профильной плоскости. В этом случае размер В (для фронтальной диметрической проекции — D/2) откладывают по оси у, а размер S — по оси г. В этой проекции сокращаются в два раза также стороны шестиугольника, расположенные параллельно оси у (размер В/4).

Пример З. Построение аксонометрических проекций призм (рис. 3.48 и рис. 3.49).

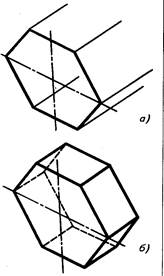
Рис. 3.48.

Изображение правильной шестиугольной призмы в изометрической проекции

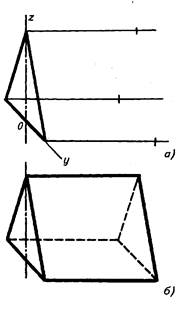
Рис. 3.49.

Изображение треугольной призмы во фронтальной диметрической проекции

Сначала строят проекции видимого основания, например, в плоскости у 0 z Через его вершины проводят прямые, параллельные оси х', и отклады- вают на них высоту (длину) призмы (рис. 3.48, а и рис. 3.49, а).

Полученные точки соединяют отрезками прямых и обводят линии видимо- го и невидимого контура (рис. 3.48, б и рис. 3.49, б).

Пример 4. Построение аксонометрических проекций правильных пирамид (рис. 3.50 и рис. 3.51).

Сначала строят проекцию основания пирамиды и через точку 0' — центр тяжести полученной на плоскости фигуры — проводят ось z'. От точки 0 по оси z' откладывают высоту пирамиды (рис. 3.50, а и рис. 3.51, а).

Полученную точку (проекцию вершины пирамиды) соединяют с проекциями вершин основания. В заключение обводят линии видимого и невидимого контура (рис. 3.50, б и рис. 3.51, б).

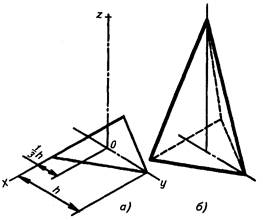
Рис. 3.50.

Изображение правильной треугольной пирамиды в изометрической проекции

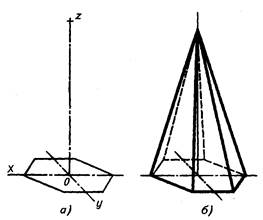
Рис. 3.51.

Изображение правильной шестиугольной пирамиды во фронтальной диметрической проекции