Техническая работа

Внутренняя энергия. Известно, что эквивалентность теплоты и работы является опытным подтверждением всеобщего закона сохранения и превращения энергии, согласно которому энергия не исчезает и не возникает вновь, она лишь переходит в разлитых физических (а также химических) процессах из одного вида к другой.

Закон сохранения и превращения энергии в применении к понятиям термодинамики носит название первого закона термодинамики.

Опыт показывает, что подвод теплоты Q к какому-либо телу гак же, как и отвод теплоты) обычно связан с изменением температуры тела Т и его объема V.

Изменение температуры обусловлено изменением энергии движения молекул вещества. Этот вид энергии называется внутренней энергией, под которой понимается сумма кинетической и потенциальной энергий атомов и молекул тела. В общем случае внутренняя энергия тела складывается из кинетической энергии поступательного, вращательного и колебательного движения молекул, потенциальной энергии сил сцепления (отталкивания) между молекулами, внутримолекулярной, внутриатомной и внутриядерной энергии.

Если количество внутренней энергии рабочего тела до начала подвода теплоты к этому телу обозначить через U_1ъа количество внутренней энергии этого же тела после окончания подвода теплоты — через U₂, то результатом процесса будет изменение внутренней энергии:

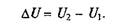
Для определения разности DU нет необходимости знать, по какому закону происходит подвод теплоты к телу. Поэтому внутренняя энергия тела может быть отнесена к группе параметров состояния.

Первый закон термодинамики.Изменение объема тела при нагревании (или охлаждении) связано с работой, которую производят возникающие в этом процессе силы, проявляющиеся в форме давления на поверхность тела. Работа этих сил в процессе подвода теплоты Q называется внешней работой L. Отсюда следует, что затрата теплоты Q при изменении температуры и объема тела связана с изменением внутренней энергии AU и совершением внешней работы L, следовательно, в соответствии с законом сохранения энергии

Соотношение (2.1) называют обычно аналитическим выражением первого закона термодинамики для неподвижного тела. Это соотношение устанавливает, что в данном термодинамическом процессе теплота расходуется в двух направлениях: на изменение внутренней энергии и на совершение внешней работы.

В технической термодинамике принимают, что основной формой преобразования теплоты во внутреннюю энергию является изменение кинетической энергии движения молекул (как функции изменения температуры) и потенциальной энергии сил сцепления между молекулами (как функции изменения удельного объема): U = f (T, v).

Для идеальных газов силы сцепления между молекулами равны нулю, следовательно, внутренняя энергия таких газов зависит только от их абсолютной температуры: U = f (T).

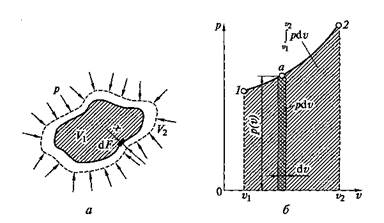
Рис. 2.1. Изменение объема газа в процессе расширения (а)и графическое изображение работы расширения (сжатия) на р—v -диаграмме (б)

Работа расширения (сжатия) неподвижного тела проявляется в изменении объема тела V под действием давления p. Например, если к газу, занимающему объем V₁(рис. 2.1, а)при давлении среды р, подвести некоторое количество теплоты Q, то можно наблюдать увеличение объема газа до величины V₂. Каждый элемент объема под действием давления р переместится при этом на величину х. Так как давление всегда направлено по нормали к поверхности, то сила, действующая на элемент поверхности dF, будет равна pdF, а элементарная работа на пути х

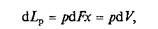
где dV= dF×x —- элементарный объем.

Очевидно, полная работа для всей поверхности тела при изменении объема от V₁до V₂

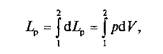
или для 1 кг газа

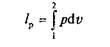
и

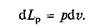
Работа расширения как функция давления и объема может быть графически изображена в координатах p и v (рис. 2.1,б). Если в данном процессе зависимость давления от объема изображается кривой 1—2, то для элементарного объема dv величина элементарной работы dI_p может быть выражена элементарной площадкой dI_p = pdv, а вся работа расширения при изменении объема 1 кг газа от v₁до v₂ определяется по формуле

и равна площади, ограниченной линией процесса 1—2 и осью абсцисс.

Уравнение первого закона термодинамики, устанавливающего связь между подведенной к телу теплотой, изменением внутренней энергии и внешней работой, при расчете на единицу массы примет следующий вид:

или в дифференциальной форме

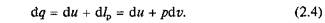
Техническая работа. Если теплота сообщается движущемуся в пространстве телу, например потоку газа или пара, текущему по каналу произвольной формы, то получаемая при этом внешняя работа, кроме работы расширения, включает еще и другие виды механической энергии. Так, если 1 кг газа или пара движется (рис. 2.2,а)от сечения 1—1 к сечению 2—2 со скоростью, изменяющейся от с₁до с₂, то в этом случае наблюдается изменение кинетической энергии от I₁= с₁²/2до I₂ = с₂²/2. Кроме того, подходя к сечению 1—1 (или покидая сечение 2—2), каждый элемент объема вытесняет равный ему объем вещества, т.е. совершает так называемую работу проталкивания.

По аналогии с работой расширения можно получить, что теплота, подводимая к движущему телу (газу или пару),

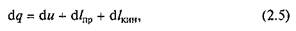
где dи – изменение внутренней энергии; dI_np – изменение работы проталкивания; dI_кин – изменение кинетической энергии.

Уравнение (2.5) является аналитическим выражением первого закона термодинамики для потока газа.

Изменение кинетической энергии потока называют его технической работой I_техн = DI_кин. Из уравнения (2.4) после ряда замен и преобразований получаем

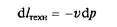
(знак минус указывает на уменьшение объема при росте значений давления).

В итоге полная техническая работа (рис. 2.2,б), совершаемая в процессе 1– 2,

определится как площадь, ограниченная линией процесса 1–2 и осью р (напомним, что величина I_р определялась как площадь, ограниченная линией процесса и осью v).

2.3. Теплоемкость, энтальпия и энтропия. Второй закон