Метод дискретных моделей
Метод основан на использовании дискретных моделей индуктивного и емкостного элементов и позволяет свести численный анализ динамических процессов в нелинейных цепях к последовательному расчету на каждом шаге нелинейных резистивных цепей.
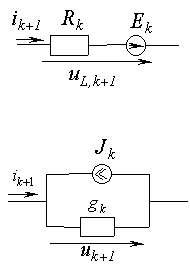
Дискретные модели вытекают из неявных алгоритмов, в частности из обратной формулы Эйлера. Эти модели, полученные на основе неявного алгоритма Эйлера, а также выражения для параметров входящих в них элементов приведены в табл. 1.
Таблица 1. Дискретные модели индуктивного и емкостного элементов
| Тип элемента | Аналитические соотношения | Дискретная модель | ||||
|
| 
|
Примечание: если емкостный и индуктивный элементы линейные и 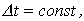 то
то 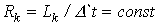 и
и 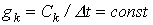 .
.
Метод дискретных моделей хорошо поддается машинной алгоритмизации и используется для расчета сложных нелинейных цепей на ЭВМ. Для достаточно простых схем он может быть реализован ’’вручную’’.
Последовательность расчета нелинейной цепи методом дискретных моделей иллюстрируется приведенным ниже примером решения задачи.
В цепи на рис. 3 предыдущей задачи ЭДС источника Е = 1В; 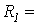 1Ом;
1Ом; 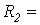 4 Ом. Вебер - амперная характеристика нелинейной катушки индуктивности аппроксимирована выражением
4 Ом. Вебер - амперная характеристика нелинейной катушки индуктивности аппроксимирована выражением 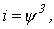 где ток – в амперах, потокосцепление – в веберах.
где ток – в амперах, потокосцепление – в веберах.
Рассчитать ток i в цепи после замыкания ключа
.
Решение
1. Нарисуем расчетную дискретную схему замещения цепи (см. рис. 4).
Для этой схемы справедливо
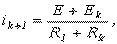
| (6) |
 где в соответствии с табл. 1
где в соответствии с табл. 1
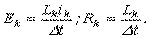
Значение дифференциальной индуктивности нелинейной катушки на k-м шаге
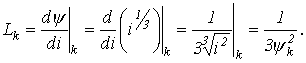
| (7) |
2. Выберем шаг интегрирования 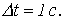 На основании закона коммутации
На основании закона коммутации 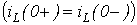
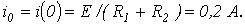 Тогда
Тогда 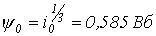 и в соответствии с (7)
и в соответствии с (7) 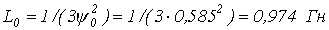 . Параметры элементов схемы замещения:
. Параметры элементов схемы замещения: 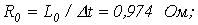
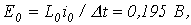 откуда на основании (6)
откуда на основании (6)
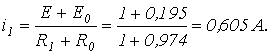
На следующем шаге 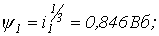 тогда
тогда 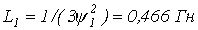 и параметры элементов схемы замещения
и параметры элементов схемы замещения 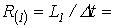
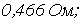
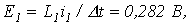 откуда
откуда
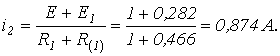
Результаты пошагового расчета согласно приведенному алгоритму представлены в табл. 2 .
Таблица 2. Результаты расчета
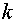
| 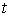
| 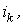
| 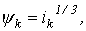
| 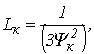
| 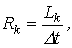
| 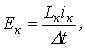
| 
|
| с | А | Вб | Гн | Ом | В | А | |
| 0,2 | 0,585 | 0,974 | 0,974 | 0,195 | 0,605 | ||
| 0,605 | 0,846 | 0,466 | 0,466 | 0,282 | 0,874 | ||
| 0,874 | 0,956 | 0,365 | 0,365 | 0,319 | 0,966 | ||
| 0,966 | 0,989 | 0,341 | 0,341 | 0,329 | 0,99 | ||
| 0,99 | 0,997 | 0,335 | 0,335 | 0,332 | 0,998 |
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Матханов П.Н.Основы анализа электрических цепей. Нелинейные цепи.: Учеб. для студ. электротехн. спец. вузов. 2-е изд., перераб. и доп. –М.: Высш. шк., 1986. –352с.
Контрольные вопросы
- Какие графические методы применяются для расчета переходных процессов в нелинейных цепях? В чем их сущность?
- Какие методики применяются для составления уравнений состояния?
- Сформулируйте этапы составления уравнений состояния на основе принципа наложения.
- В чем заключается сущность метода дискретных моделей?
- Нарисуйте дискретные модели нелинейных индуктивного и емкостного элементов и напишите соответствующие им аналитические соотношения.
Дата добавления: 2015-10-13; просмотров: 695;

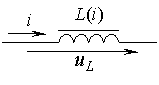
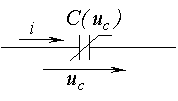
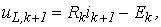 где
где 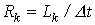 ;
;
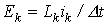 ;
;
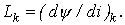
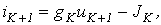 где
где 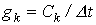 ;
;
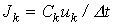 ;
;
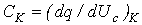 .
.