Графические методы расчета. При использовании этих методов задача решается путем графических построений на плоскости

При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.

а) Цепи с последовательным соединением резистивных элементов.

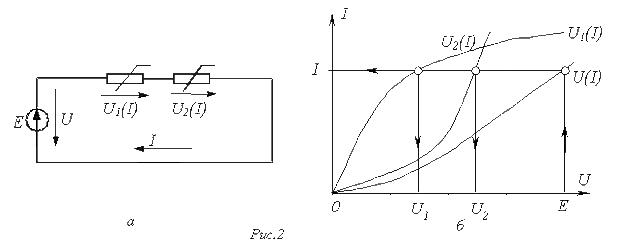
При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ 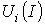отдельных резисторов в системе декартовых координат 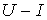строится результирующая зависимость 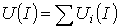. Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью 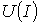. Из точки пересечения перпендикуляра с кривой 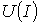опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей 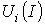определяются напряжения 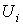на отдельных резистивных элементах.

Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.

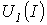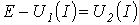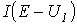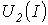Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом –методом пересечений.В этом случае один из нелинейных резисторов, например, с ВАХ на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения точка а (см. рис. 3) пересечения кривых и определяет режим работы цепи. Кривая 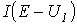строится путем вычитания абсцисс ВАХ 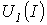из ЭДС Е для различных значений тока.

Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.

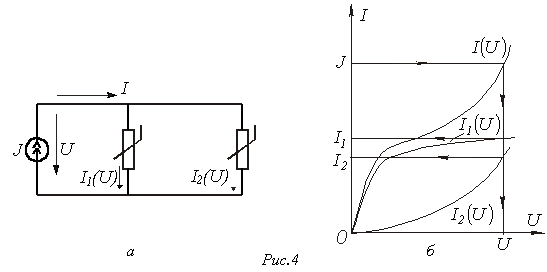
б) Цепи с параллельным соединением резистивных элементов.

При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ 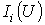отдельных резисторов в системе декартовых координат 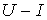строится результирующая зависимость 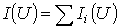. Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ 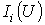), из которой восстанавливается перпендикуляр до пересечения с зависимостью 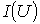. Из точки пересечения перпендикуляра с кривой 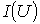опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей 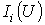определяются токи 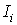в ветвях с отдельными резистивными элементами.

Использование данной методики иллюстрируют графические построения на рис. 4,б, соответствующие цепи на рис. 4,а.

в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.

1. Расчет таких цепей производится в следующей последовательности:

Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).

2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.