Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
Таблица 1. Таблица соединений
| u | |||
| -1 | |||
| J |
Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, ориентация которых совпадает с направлением обхода контура, и со знаком «-» ветви, имеющие противоположную ориентацию.
Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму.
В рассматриваемом случае (равенство 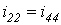 тривиально)
тривиально)
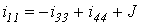 ,
,
откуда в соответствии с нумерацией токов в исходной цепи
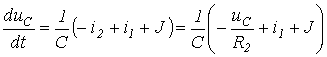 .
.
При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками, противоположными табличным:
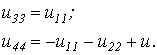
| (7) |
Эти уравнения совпадают соответственно с соотношениями (6) и (5).
Из (7) непосредственно вытекает
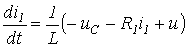 .
.
Таким образом, формализованным способом получены уравнения, аналогичные составленным выше с использованием законов Кирхгофа.
Литература
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Матханов П.Н.Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. радиотехн. спец. вузов. 3-е изд., перераб. и доп. –М.: Высш. шк., 1990. –400с.
Контрольные вопросы и задачи
- Какой принцип лежит в основе метода расчета переходных процессов с использованием интеграла Дюамеля, и для каких цепей может быть использован данный метод?
- В каких случаях целесообразно использовать метод расчета с использованием интеграла Дюамеля?
- В цепи на рис. 3 при
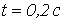 напряжение на входе цепи мгновенно спадает до нуля. Определить ток в цепи.
напряжение на входе цепи мгновенно спадает до нуля. Определить ток в цепи.
Ответ: 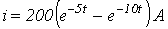 при
при 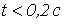 ;
; 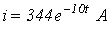 при
при 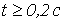 .
.
- Какие требования и почему выдвигаются к уравнениям состояния?
- Что включает в себя система уравнений при расчете переходного процесса в цепи методом переменных состояния?
- Перечислите основные этапы методики составления уравнений состояния.
- Записать матрицы А и Вдля цепи на рис. 5, если
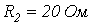 ,
, 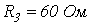 ,
, 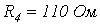 ,
, 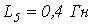 ,
, 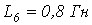 ,
, 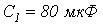 .
.
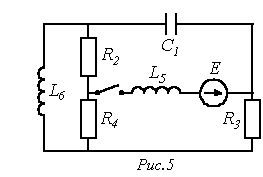
| Ответ: | А | 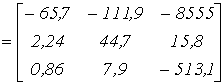
| ; |
| В | 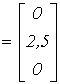
|
Дата добавления: 2015-10-13; просмотров: 990;
