УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

Выведем уравнение одномерной упругой волны, которую называют часто бегущей волной. Пусть в некоторой точке О (рис. 2) в упругой среде находится источник волн, который выполняет колебания по закону:

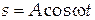
(1)

Рис.2

Очевидно, что частица среды, которая находится на расстоянии х от источника волн, начнет колебания только тогда, когда к ней дойдет волновой процесс, который распространяется в среде, т.е. колебание рассмотренной нами частицы будут происходить по закону (1), но с опозданием на промежуток времени

,

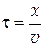где v – скорость распространения волны.

Таким образом, колебания частицы, которая находится в точке М, будут происходить по закону

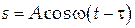
или

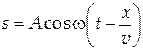
(2)

Здесь s – сдвиг частицы в точке пространства с координатой x в момент времени t.

Уравнение (2) представляет собой уравнение бегущей волны. Из этого уравнения видно, что сдвиг частицы среды является периодической функцией как пространственной, так и временной координаты.

Аргумент косинуса в (2) представляет собой фазу волны.

Кратчайшее расстояние между точками, которые колеблются в одинаковой фазе, называется длиной волны. Длина волны численно равняется расстоянию, на которое распространяется волна за время, равное периоду колебаний:

,

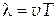(3)

где T – период колебаний, 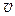– скорость распространения волны.

Преобразуем фазу волны таким образом:

.

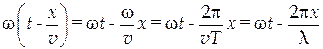(4)

С учетом (4) уравнение волны (2) можно представить в виде:

.

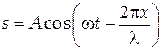(5)