Определитель матрицы

Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.

Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 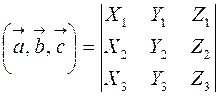, или в свернутой форме 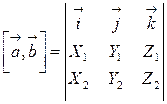. Предыдущая формула получается разложением определителя по первой строке.

Возьмем теперь квадратную матрицу 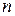-го порядка

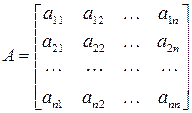
(9.2)

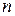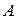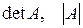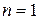Для записи определителя -го порядка матрицы будем применять обозначения . При матрица 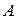состоит из одного элемента и ее определитель равен этому элементу. При 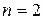получаем определитель .

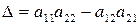Минором 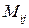элемента 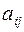матрицы 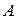называют определитель матрицы -го порядка, получаемого из матрицы 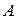вычеркиванием 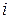-той строки и 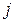-го столбца.

Пример 7. Найти минор 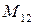матрицы:

.

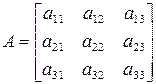По определению, минор 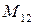элемента 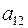есть определитель матрицы, получаемой из матрицы 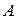вычеркиванием первой строки и второго столбца. Следовательно, .

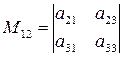Алгебраическим дополнением элемента 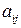матрицы 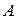называется минор 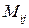, взятый со знаком 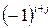. Алгебраическое дополнение элемента 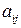обозначается 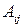, следовательно, .

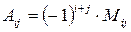Пример 8. Найти алгебраическое дополнение элемента 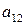матрицы 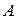из примера 7.

.

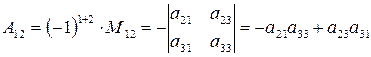Определителем квадратной матрицы 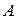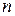-го порядка 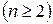называется число:

,

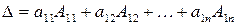(9.3)

где 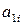‑ элементы первой строки матрицы (9.2), а 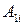их алгебраические дополнения .

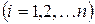Запись по формуле (9.3) называется разложением определителя по первой строке.

Рассмотрим свойства определителей.