Линейные операции над векторами
Сложение вектора производится по правилу параллелограмма: векторы 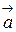 и
и 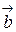 сносятся в общую точку
сносятся в общую точку 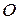 (рис. 4.1), на них строят параллелограмм
(рис. 4.1), на них строят параллелограмм 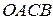 и его диагональ
и его диагональ 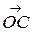 называют суммой векторов
называют суммой векторов 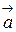 и
и 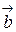 .
.

Рис. 4.1.
Поскольку вектор 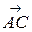 равен
равен 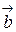 , то можно дать другое правило нахождения суммы
, то можно дать другое правило нахождения суммы 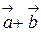 (правило треугольника): суммой векторов
(правило треугольника): суммой векторов 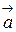 и
и 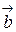 является вектор, идущий из начала
является вектор, идущий из начала 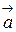 в конец
в конец 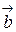 , если вектор
, если вектор 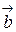 приложен к концу вектора
приложен к концу вектора 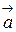 , т.е.:
, т.е.:
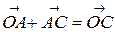
| (4.1) |
Это правило распространяется на любое число слагаемых: если векторы 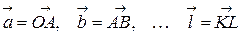 образуют ломаную
образуют ломаную 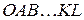 , то суммой этих векторов является вектор
, то суммой этих векторов является вектор 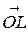 , замыкающий эту ломаную, т.е.:
, замыкающий эту ломаную, т.е.:
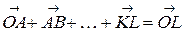
| (4.2) |
В частности, если ломаная замыкается, т.е. 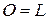 , то сумма ее звеньев равна нуль-вектору
, то сумма ее звеньев равна нуль-вектору 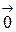 .
.
Сложение векторов подчиняется обычным законам сложения ‑ сочетательному и переместительному, а также обладает обратной операцией – вычитанием.
Разностью двух векторов 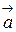 и
и 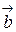 , отложенных от одной точки
, отложенных от одной точки 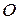 является вектор, направленный из конца вычитаемого вектора
является вектор, направленный из конца вычитаемого вектора 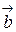 в конец уменьшаемого вектора
в конец уменьшаемого вектора 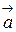 , т.е.
, т.е. 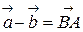 (Рис. 4.2.). Это правило следует из формулы (1): т.к.
(Рис. 4.2.). Это правило следует из формулы (1): т.к. 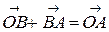 , то
, то 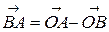 .
.
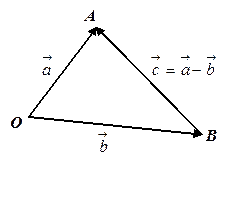
Рис. 4.2.
Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры).
Вектор 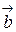 равен
равен 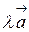 , где
, где 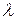 ‑ некоторое число, если:
‑ некоторое число, если:
1. 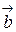 коллинеарен
коллинеарен 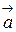 ;
;
2. длина вектора 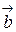 отличается от длины вектора
отличается от длины вектора 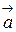 в
в 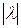 раз, т.е.
раз, т.е. 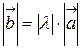 ;
;
3. при 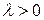 ,
, 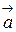 и
и 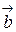 направлены в одну сторону, при
направлены в одну сторону, при 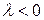 ‑ в разные.
‑ в разные.
Произведение вектора на скаляр обладает следующими свойствами:
1. 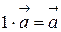 ;
;
2. 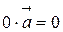 ;
;
3. 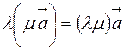 ;
;
4. 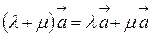 ;
;
5. 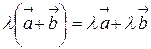 .
.
Дата добавления: 2015-10-09; просмотров: 818;
