О расчете конструкций по методу предельного равновесия

Этот метод разработан учеными во главе с профессором А. А. Гвоздевым и используется для расчета несущей способности статически неопределимых железобетонных конструкций. Использование этого метода приводит к экономическому эффекту за счет уменьшения количества арматуры, благодаря перераспределению усилий (изгибающих моментов) с учетом пластических деформаций бетона и арматуры.

В статически определимой свободно лежащей балке в стадии близкой к разрушению и достижению в арматуре предела текучести образуется участок с большими местными деформациями, называемый пластическим шарниром.

В балке, защемленной на опорах, с появлением пластического шарнира, повороту частей балки препятствуют лишние связи (защемление на опорах). Поэтому при дальнейшем увеличении нагрузки разрушение в пластическом шарнире не произойдет, пока не появятся новые пластические шарниры и выключатся лишние связи. В статически неопределимой системе возникновение пластического шарнира равносильно выключению лишней связи и снижению на одну степень статической неопределимости системы. Потеря геометрической неизменяемости системы может наступить лишь с образованием трех пластических шарниров – на обеих опорах и в пролете. Последовательность перераспределения изгибающих моментов под действием силы F₀ можно рассмотреть на примере балки, защемленной на двух опорах (рис.23,а).

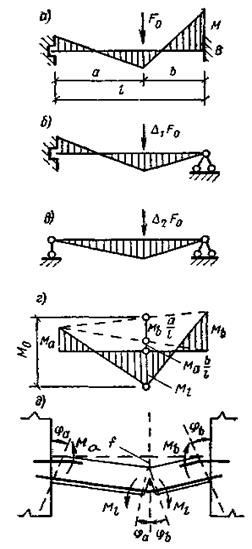Рис.23. Эпюры перераспределения изгибающих моментов в статически неопределимой балке

С появлением пластического шарнира на опоре B при нагрузке F₀ балка как бы теряет одну связь и становится шарнирной на опоре B, но защемленной на опоре A (рис.23,б). Нагрузка увеличивается на Δ₁F₀, теряем одну связь на опоре A, и балка превращается в свободно опертую (рис.23, в). При дополнительной нагрузке Δ₂F₀ образуется пластический шарнир в пролете и балка разрушается. Полная нагрузка в балке составит .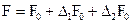

Предельные расчетные моменты в пластических шарнирах равны M _а – на опоре A; M _b – на опоре B, M _l – в пролете (рис.23, г). В предельном равновесии изгибающие моменты в балке можно найти статическим или кинематическим способом.

1.Статический способ:

Пролетный момент: ;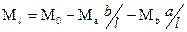

уравнение равновесия ;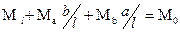

где M₀ – момент в статически определимой свободно лежащей балке .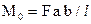

2.Кинематический способ

Балку в предельном равновесии рассматривают как систему жестких звеньев, соединенных друг с другом в местах излома пластическими шарнирами (рис.23, д).

Если прогиб балки под силой F равен f, то углы поворота звеньев

; .

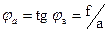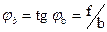Исходим из равенства работ внешних и внутренних усилий .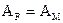

Виртуальная работа силы F: .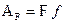

Работа внутренних усилий (изгибающих моментов) в пластических шарнирах - равна сумме моментов на углы поворотов звеньев: .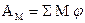

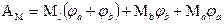
Подставляем 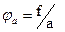и ;

;

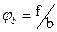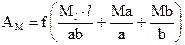Уравнение виртуальных работ

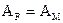
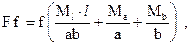
отсюда 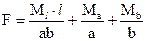- сила, при которой разрушится данная конструкция.

Если умножить правую и левую часть уравнения на 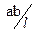, то получим уравнение равновесия такое же, как при расчете статическим способом.