Точность определения координат точек объекта по стереопаре снимков.

Для предрасчета точности определения координат точек местности по стереопаре аэрофотоснимков, учитывая, что углы наклона снимков не превышают 1°- 3°, а базис фотографирования практически горизонтален, воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки (1.8.4):

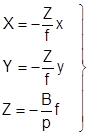. (1.8.4)

Сначала получим среднюю квадратическую ошибку определения высоты точки Z местности. Для этого продифференцируем третью формулу выражения (1.8.4) по аргументу р.

.

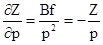Заменим величину р на b – базис в масштабе снимка.

Рис.1.16.1

О₁и О₂ – главные точки снимка.

В результате получим .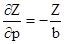

Перейдя к средним квадратическим ошибкам, получим формулу:

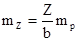. (1.16.1)

Для получения средних квадратических ошибок определения координат Х и Y точки местности продифференцируем первые две формулы выражения (1.8.4) по аргументам x, y, Z и перейдем к средним квадратическим ошибкам.

В результате получим

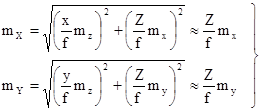. (1.16.2)

В качестве примера вычислим величины m_X, m_Y и m_Z точек местности, определенных по стереопаре снимков масштаба 1:5000, полученной АФА с f =150 мм и форматом кадра 23х23 см, с продольным перекрытием 60%.

Будем считать, что на стереопаре снимков точки были измерены с ошибками 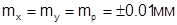. В этом случае высота фотографирования 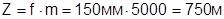, а базис фотографирования в масштабе снимка

.

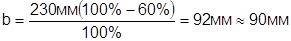Средние квадратические ошибки определения координат точки местности, вычисленные по формулам (1.16.1) и (1.16.2) будут равны:

.

4.1 МЕТОД ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

Метод имитационного моделирования - один из наиболее мощных методов исследования реально существующих и проектируемых объектов самой различной природы и степени сложности. Сущность это метода состоит в построении так называемой имитационной модели исследуемого объекта и в целенаправленном экспериментировании с такой моделью для получения ответов на те или иные вопросы.

Имитационные модели могут быть представлены самыми различными устройствами (приспособлениями), начиная листом бумаги и карандашом и кончая современными ЭВМ.

В литературе метод имитационного моделирования встречается также под названием метода цифрового, машинного, программного, статистического, вероятностного, автоматного или динамического моделирования и метода машинной имитации. В зарубежной научной литературе на английском языке термину "имитационное моделирование" соответствуют "computer simulation" и "digital simulation".

Метод имитационного моделирования может рассматриваться как своеобразный экспериментальный метод исследования. От обычных, прямых экспериментальных методов он отличается тем, что при его использовании испытаниям подвергается не сам объект, а реализованная на ЭВМ его математическая модель. Оперирование с математической моделью осуществляется при этом подобно тому, как это делалось бы (пусть даже чисто умозрительно) с исследуемым объектом; результаты моделирования обрабатываются и истолковываются так же, как если бы это были данные натурных испытаний объекта. При исследовании имитационной модели могут быть применены хорошо развитые методы планирования эксперимента и обработки экспериментальных данных.

Сугубо экспериментальный характер метода имитационного моделирования обусловлен тем обстоятельством, что имитационная модель объекта, предоставляя возможность экспериментирования с ней, не позволяет получить аналитическое решение задач исследования.

Предположим, что исследование некоторого реального объекта, например, фотограмметрической сети производится с целью установления зависимости одного или нескольких показателей, оценивающих функционирование объекта, а именно, процесса построения и уравнивания сети, от параметров объекта, которыми являются характеристики сети и параметров внешних воздействий - источников погрешностей. Если предположить, что исследуемый объект (фотограмметрическая сеть, а, конкретно, ее точность) и внешние воздействия (возмущения идеальных исходных данных) являются вероятностными по своей природе, то может ставиться задача нахождения аналогичной зависимости между средними значениями (математическими ожиданиями) указанных величин.

Как и в случае одиночного натурного испытания объекта, одиночное испытание ("проигрывание") имитационной модели на ЭВМ позволяет получить лишь одно значение того или иного показателя, соответствующее данному варианту конкретных значений параметров объекта и внешних воздействий. "Проигрывание" модели при различных вариантах значений этих параметров дает соответствующий ряд значений каждого из показателей. Если исследуемый объект и его имитационная модель имеют вероятностный характер функционирования, то для нахождения одного среднего значения какого - либо показателя необходимо осуществить многократное "проигрывание" модели при фиксированных средних значениях параметров объекта и внешних воздействий, а полученные случайные значения показателя подвергнуть статистической обработке.

Результаты имитационных экспериментов могут быть оформлены затем в виде графиков или таблиц, в которых каждому варианту значений (средних значений) параметров объекта и внешних воздействий поставлены в соответствие определенные значения (средние значения) показателей, оценивающих функционирование объекта. Однако зависимости между теми же величинами в аналитическом виде с помощью имитационной модели не могут быть получены. Можно лишь попытаться путем дальнейшего анализа имеющихся данных подобрать аналитические выражения, аппроксимирующие экспериментально найденные зависимости. Невозможность непосредственного получения аналитического решения задач исследования является наиболее существенным недостатком рассматриваемого метода.

Несмотря на отмеченный недостаток, метод имитационного моделирования представляет собой более мощный инструмент исследования, чем классический аппарат математического анализа. Это объясняется тем, что имитационная модель исследуемого объекта может быть построена и экспериментально изучена и в том случае, если объект не поддается изучению аналитическими методами. Поскольку аналитическое исследование объекта всегда предпочтительнее любого другого способа его изучения, то к методу имитационного моделирования обычно обращаются лишь тогда, когда аналитическое решение задачи исследования данного объекта существенно затруднено или невозможно.

Как следует из определения сущности метода имитационного моделирования, процедура использования этого метода включает два основных этапа: построение имитационной модели исследуемого объекта и целенаправленное экспериментирование с такой моделью. Очевидно, что от качества построенной модели во многом зависит эффективность решения задач исследования.

Исследуемые системы могут быть по своей природе непрерывными и дискретными. Нетрудно видеть, что на ЭВМ наиболее "естественным" образом имитируется функционирование дискретных систем. Для имитации процесса функционирования той или иной непрерывной системы используются специфические приемы, позволяющие, в конечном счете, осуществлять на ЭВМ дискретную аппроксимацию указанного процесса с приемлемой степенью точности.

Отметим, что, применяя метод имитационного моделирования при проектировании и построении фотограмметрических сетей, мы будем рассматривать лишь дискретную модель процесса.

Остановимся теперь несколько подробнее на имитационной модели. Как было показано выше, при использовании метода имитационного моделирования процесс функционирования исследуемого объекта воспроизводит ЭВМ, в которую введена специальная программа. В соответствии с этой программой ЭВМ осуществляет пошаговое определение значений характеристик состояния абстрактной системы, выступающей в качестве формализованного представления (математической модели) исследуемого объекта. Указанную специальную программу обычно называют моделирующей программой, или моделирующим алгоритмом.

Несмотря на отмеченное обстоятельство, имитационной моделью объекта обычно называют не ЭВМ с введенной в нее моделирующей программой, а саму моделирующую программу. Это объясняется, прежде всего, тем, что построение любой имитационной модели сводится, в конечном счете, лишь к разработке моделирующей программы, а ЭВМ для экспериментирования, естественно предполагается уже имеющейся в наличии, и она (ЭВМ) рассматривается лишь в качестве некоторого вспомогательного устройства, обеспечивающего функционирование самой имитационной модели.

Заметим, что в ходе выполнения моделирующей программы ЭВМ не только воспроизводит процесс функционирования исследуемого объекта, но и выполняет еще и ряд других действий, направленных на обеспечение самой возможности такого воспроизведения и получения либо искомых решений поставленных задач исследования, либо исходной информации для решения тех или иных задач. Сюда входит формирование начальных значений параметров модели и, если это необходимо, статистическая, или какая-либо иная обработка результатов моделирования, а также формирует результаты с соблюдением заданной формы их вывода (таблицы, графики и т.п.). В случае вероятностной имитационной модели и при решении методом имитационного моделирования различного рода оптимизационных задач ЭВМ в ходе выполнения соответствующей моделирующей программы может, в частности, осуществлять многократное воспроизведение процесса функционирования исследуемого объекта в соответствии с заданными инструкциями и т.д.

Любая моделирующая программа может быть оформлена на одном из универсальных языков программирования высокого уровня (Паскаль, ФОРТРАН, С++ и др.). В последнее время в практике имитационного моделирования для составления моделирующих программ все чаще используются и так называемые языки моделирования. Это специализированные языки высокого уровня, программы на которых позволяют воспроизводить на ЭВМ процессы функционирования строго определенных типов абстрактных систем.

Использование языков моделирования облегчает и ускоряет создание программ имитации функционирования абстрактных систем соответствующих типов. Однако трансляторы с таких языков пока не получили достаточного распространения. Кроме того, языки моделирования чаше всего ориентированы на решение определенного и иногда довольно узкого круга задач, что резко снижает их применение. Поэтому в настоящее время моделирующие программы обычно оформляются все же на тех или иных универсальных языках программирования.

4.2 ПОСТРОЕНИЕ МОДЕЛЕЙ МЕСТНОСТИ И СНИМКОВ ЗАДАННЫХ ПАРАМЕТРОВ

Рассмотрим технологию автоматизированного создания математических моделей местности и снимков с параметрами, соответствующими условиям решения конкретных задач. Для вычисления координат точек макетного снимка обычно используются уравнения коллинеарности. При этом подбираются такие элементы ориентирования снимков и координаты точек местности, при которых геометрические параметры создаваемых макетов соответствуют заданным. Построения ведутся по принципу: "точка местности - точка снимка". Выбор элементов внутреннего и внешнего ориентирования снимков не вызывает затруднений. Гораздо труднее подбирать координаты точек местности, т.к. до вычисления их координат на снимке трудно предсказать точное местоположение точек на снимке, а, следовательно, трудно автоматизировать процесс создания макетных снимков с заранее заданной схемой расположения точек. При таком подходе координаты точек местности могут оказаться такими, что точки окажутся вне формата снимков, то есть не изобразятся на нем.

Зададимся следующей задачей: точки на снимках должны по возможности изображаться в заранее определенных местах. Для этого используем обратные к (1.2) зависимости:

X = X_S + (Z - Z_S) X' / Z'

Y = Y_S + (Z - Z_S) Y' / Z' (4.2.1)

Зависимости (4.2.1) позволяют создавать модели местности и снимков по принципу: "точка снимка - точка местности". Это возможно благодаря тому, что правые части уравнений (3.3) содержат координаты точек снимка x, y, которые являются исходными данными и задаются в соответствии со схемой желаемого расположения точек на снимке. Для вычисления плановых координат точек местности, соответствующим точкам на снимке, остается задать элементы внешнего ориентирования и координаты Z точек местности, которые определяются в зависимости от характера рельефа моделируемой местности. Линейные элементы внешнего ориентирования зависят от масштаба снимков, фокусного расстояния, их продольного и поперечного перекрытия. Все эти величины необходимо назначить, однако высоты точек местности, а также углы наклона и разворота снимков удобно задавать случайным образом, указав только пределы их изменения. В случае использования данных о местности многие величины (например, сведения о рельефе местности) можно взять из географической информационной системы.

Для обеспечения необходимого продольного и поперечного перекрытия снимков при выборе линейных элементов внешнего ориентирования воспользуемся формулами:

bX = lX (100-p)/100

bY = lY (100-q)/100 . (4.2.2)

Элементы XS , YS первого снимка блока задаются произвольно, а для остальных снимков XS , YS получаются последовательным прибавлением bX , bY , вычисленных по формулам (4.5):

XSi = XSi+1 + bX

YSi = YSi+1 + bY . (4.2.3)

Координаты ZS всех снимков равны:

ZS = f m . (4.2.4)

В линейные элементы внешнего ориентирования снимков обычно вводятся случайным образом поправки, имитирующие реальные изменения этих элементов, имеющие место при съемке местности.

Принципиальная схема, отражающая последовательность построения модели маршрутной сети и соответствующей ей модели местности приведена на рис. 4.1.

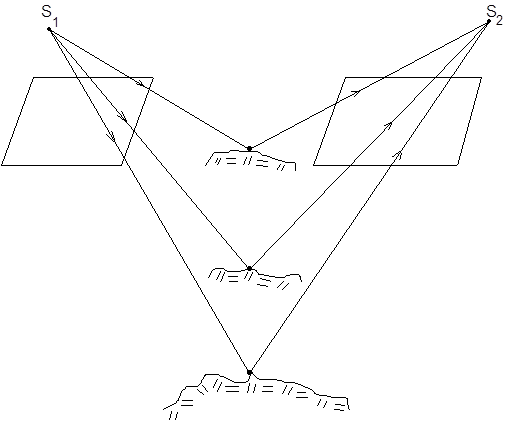
Рис. 4.2.1

Здесь стрелками указана последовательность ее построения. Для лучей, направленных к точкам местности, применяются уравнения (4.2.1), при этом координаты точек на снимке определяются по его формату и схеме расположения точек, а высоты задаются либо случайным образом, либо, если имеется такая возможность, определяются по данным географической информационной системы, как и было указано выше. Для лучей, направленных к центрам проекций снимков, используются зависимости (1.2). Чередуя "прямую" и "обратную" проекции, можно продолжать построение модели маршрута сколь угодно.

Соблюдение неизменности числа и расположения точек на каждой стереопаре гарантировано, так как при каждой "прямой" проекции координаты точек снимка берутся с одной и той же схемы, которая представляет собой входной файл программы. Этот файл может быть отредактирован и, соответственно, может быть изменено количество и расположение точек на стереопаре, величины продольного и поперечного перекрытия снимков и т.д., при помощи любого экранного редактора текстов. Пример содержимого такого файла приведен ниже.

По изложенному принципу строятся модели не только маршрутных, но и блочных сетей. Для этого необходимо указать соответствующее число маршрутов.

Form=18 x 18 F=100.000mm M= 10000 Y Str=01 Plt=03

* *

O O

* *

Г

O O

* *

Теперь остается только назначить некоторые точки сети опорными. Для этого на схеме эти точки указываются отличным от "обычных" точек символом, а так же указывается (в этом же файле, но вне схемы) частота появления плановых и высотных точек вдоль маршрута и по блоку в снимках.

Итак, основными этапами вычислений являются:

- ввод необходимой числовой и символьной (схема расположения точек на снимке) информации;

- анализ символьной информации (поиск точек сети, опорных точек и символа, по которому определяется продольное и поперечное перекрытия снимков) и преобразование ее в числовую форму (координаты точек на схеме, а значит и на снимках для "прямой" проекции и величины перекрытий снимков);

- построение модели местности и сети, вычисление координат точек на снимках, на которых они должны изобразиться ("обратная" проекция);

- введение случайных и систематических ошибок заданной величины в эти координаты и назначение опорных точек.

Далее полученные данные передаются в программу построения и уравнивания фотограмметрической сети.

ПРОСТРАНСТВЕННАЯ ФОТОТРИАНГУЛЯЦИЯ

1.1. Назначение и классификация методов пространственной аналитической фототриангуляции

Фототриангуляция выполняется с целью сгущения опорной геодезической сети по снимкам. В результате фототриангуляции определяются элементы внешнего ориентирования снимков и геодезические координаты и высоты опорных точек в системе координат объекта.

Эти данные используются в качестве опорной и контрольной информации при выполнении процессов обработки стереопар или одиночных снимков на фотограмметрических приборах и системах.

В настоящее время построение фототриангуляции осуществляется только аналитическим методом, а измерения снимков производится на стереокомпараторах, аналитических и цифровых стереофотограмметрических системах.

Фототриангуляцию можно разделить на:

- маршрутную, в которой построение сети фототриангуляции производится по снимкам, принадлежащим одному маршруту;

- блочную, в которой сеть фототриангуляции строится из отдельных стереопар или снимков, принадлежащих нескольким маршрутам.