Методы, использующие связи между элементами изображения

В этих методах сначала выделяются элементы изображений (точки, линии, полигоны, и т.д.) затем определяют характеристики (атрибуты) этих элементов, такие как длинна, ориентация, площадь, контраст, среднее значение плотности изображения и т.д.

После присвоения этих атрибутов соответствующим элементам выполняют анализ связей между этими элементами, используя теорию графов.

Эти методы применяются только для получения первого приближения отождествления одноименных точек или для общего (достаточно грубого) отождествления двух изображений. Затем целесообразно использовать площадные методы отождествления соответственных точек для более точного их определения.

Кроме рассмотренных выше методов существует еще группа методов, основанных на применении теории динамического программирования (решение уравнений с ограничениями). Однако эти алгоритмы практически не используются из-за их сложности.

Рассмотрим более детально наиболее часто применяемые на практике методы для нахождения соответственных точек на паре перекрывающихся цифровых изображений.

Методы корреляции

Если координаты точки на левом снимке известны, координаты соответственной точки на правом снимке определяют следующим образом. Выделяют фрагмент изображения на левом снимке (его часто называют эталонной матрицей) с центром в определяемой точке и как бы накладывают ее на правый снимок (матрица поиска) и перемещают по направлениям x и y с шагом один пиксель. Для каждого положения эталонной матрицы вычисляется коэффициент корреляции R. Положение матрицы, при котором значение коэффициента корреляции является максимальным, соответствует идентичной (искомой на правом снимке) точке. Таким образом, находят координаты соответственной точки на правом снимке. Коэффициент корреляции R изменяется в пределах от 0 до 1.

Коэффициент корреляции вычисляется по следующей формуле:

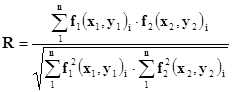(1.3.1)

Где f₁, f₂ – функции плотностей пикселей эталонной матрицы и матрицы поиска соответственно, т.е. левого и правого изображений; i – номер пикселя в матрице; n – количество пикселей в матрице; x₁,y₁ и x₂,y₂ - координаты центрального пикселя матрицы на левом и правом снимке соответственно. В частном случае, в качестве функций f₁, f₂ могут быть исходные значения плотностей пикселей, или из значения после фильтрации, или значения градиентов, и т.д. Если пара снимков отличается друг от друга по тону изображения, то в этом случае целесообразно вычислить среднее значение плотностей пикселей для каждого изображения и затем вычесть это среднее из каждого пикселя, как для левого, так и для правого снимков.

Теперь попробуем объяснить формулу (1.3.1) с геометрической точки зрения. Для этого представим все элементы эталонной матрицы и матрицы поиска как координаты векторов в n мерном пространстве (n – число элементов в эталонной матрице) и обозначим эти векторы через f₁, f₂. Из аналитической геометрии известно, что два вектора совпадают (равны) когда равны значения координат этих векторов и как следствие

угол между этими векторами равен нулю. Значение угла между двумя векторами вычисляется по известной формуле:

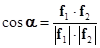(1.3.2)

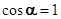когда два вектора коллинеарны (совпадают), так как 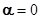. Если сравнить формулы (1.3.1) и (1.3.2) видим, что они одинаковые. Другими словами, коэффициент корреляции R представляет собой косинус угла между векторами в n пространстве, координаты которых значения плотностей пикселей. Таким образом, R=1 в том случае, когда все значения плотностей пикселей (координаты векторов) двух изображений равны между собой ( ).

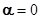Для положения эталонной матрицы, когда R принимает максимальное значение, получаем соответственную точку на правом снимке с координатами x₂,y₂. Таким образом, можно получать координаты соответственных точек на правом снимке с точностью шага перемещения эталонной матрицы по матрице поиска (в данном случае – один пиксель). Для получения координат с подпиксельной точностью можно уменьшить шаг перемещения эталонной матрицы, например, установить его равным 0.1 пикселя. В этом случае необходимо увеличить изображения в 10 раз, т.е. один пиксель исходного изображения занимает 10х10 пикселей в увеличенном изображении. На рис.1.3.1 показан пример получения увеличенного изображения в два раза. Если осуществлять корреляцию по таким изображениям, то точность определения координат будет равна 0.5 пикселя.

Существует другой метод получения подпиксельной точности. Сначала выполняют корреляцию с точностью один пиксель, затем выбирают дискретные значения коэффициентов корреляции R вокруг пикселя с R_max и описывают их непрерывной функцией. Найдя локальный экстремум этой функции можно найти координаты x,y с подпиксельной точностью. В качестве примера этой функции рассмотрим полином второй степени, который описывает поверхность образованную коэффициентами корреляции, причем раздельно по каждой координатной оси (рис.1.3.2).

Рис. 1.3.1

рис. 1.3.2

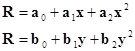( 1.3.3)

Для нахождения локального экстремума этой функции воспользуемся известным положением, что производные функции по x,y в точке экстремума R_max равны нулю, тогда соответствующие координаты можно найти по следующим формулам:

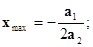
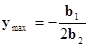(1.3.4)

Для описания поверхности, образованной коэффициентами корреляции можно применить и другой полином, например, следующий:

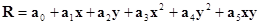(1.3.5)

Отождествление одноименных точек по методу наименьших квадратов

Этот метод основан на применении следующего уравнения:

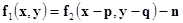(1.3.6)

Здесь x,y – координаты точки на левом снимке; p – продольный параллакс; q – поперечный параллакс; n – представляет разность шумов левого и правого изображений:

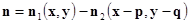(1.3.7)

Предполагая, что p и q не изменяются в пределах эталонной матрицы (фрагмента изображения вокруг измеряемой точки) можно их найти из решения уравнений (1.3.6), которые составляются для каждого пикселя фрагментов изображений. Уравнения (1.3.6) являются нелинейными относительно неизвестных. Поэтому переходят к линейным уравнениям поправок, которые можно записать в следующем виде:

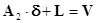, (1.3.8)

где A₂ – матрица частных производных от правого снимка по параллаксам; 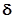- поправки к неизвестным; L – свободные члены (значения функции (1.3.6) вычисленные по приближенным значениям неизвестных); V – невязки уравнений. То есть:

; ; .

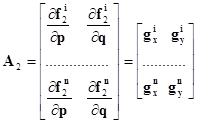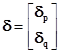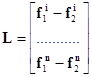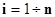, где n - количество пикселей в эталонной матрице; g_x , g_y – составляющие градиента второго изображения в пикселе i.

Решение находится как

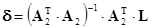(1.3.9)

Этот метод позволяет найти параллаксы с точностью 0.01 пикселя. Однако этот метод имеет и существенный недостаток – необходимость знания начальных приближений параллаксов с достаточной точностью и выполнения большого числа приближений, что существенно замедляет процесс вычислений. В качестве начальных приближений, как правило, используют значения параллаксов, полученных по методу корреляции. Для уменьшения затрат машинного времени можно заменить A₂ на A₁ , что позволит вычислить градиенты только один раз, а от приближения к приближению будет меняться только свободные члены L. Как показали практические исследования, такая замена не приводит к понижению точности решения задачи.

Это метод может быть расширен за счет включения в исходное уравнение членов, которые учитывают геометрические и фотометрических шумы двух фрагментов изображений. Как правило, для учета разности геометрических искажений двух изображений используют аффинные преобразования:

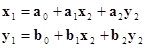(1.3.10)

а для разности фотометрических искажений используют линейные преобразования:

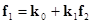(1.3.11)

Кроме того, некоторые авторы расширяют модель данного метода за счет включения в исходное уравнение уравнений коллинеарности, что позволяет выполнить отождествление сразу для множества одноименных точек, учитывая не только фотометрическое соответствие точек, но и геометрию построения фотограмметрической модели.

1.7 Формулы связи координат точек местности и их изображений на стереопаре снимков (прямая фотограмметрическая засечка).

Рис.1.7.1

p=x₁-x₂ – продольный параллакс;

q=y₁-y₂ – поперечный параллакс.

Рис.1.7.2

На рис.1.7.2 показана стереопара снимков Р₁ и Р_2, на которых точка местности М изобразилась соответственно в точках m₁ и m₂. Будем считать, что элементы внутреннего и внешнего ориентирования снимков известны.

Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков.

Из рис.1.7.2 следует, что векторы 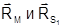определяют соответственно положение точки местности М и центра проекции S₁ снимка Р₁ относительно начала системы координат объекта OXYZ. Вектор 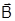определяет положение центра проекции S₂ снимка Р₂ относительно центра проекции S₁.

Векторы 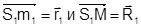определяют положение точек m₁ и М относительно центра проекции S₁. Векторы 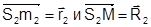определяют положение точек m₂ и М относительно центра проекции S₂.

Из рис.1.7.2 следует, что

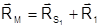(1.7.1)

Так как векторы 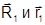коллинеарные, то

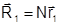; (1.7.2)

где N – скаляр.

С учетом (1.7.2) выражение (1.7.1) будет иметь вид

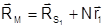. (1.7.3)

В координатной форме выражение (1.7.3) будет иметь вид

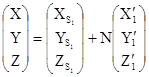; (1.7.4)

где X₁’,Y₁’,Z₁’ –координаты вектора 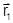в системе координат объекта OXYZ.

.

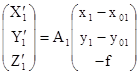Найдем значение N, входящее в выражение (1.7.4). Из рис.1.7.2 следует, что

;

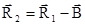или с учетом (1.7.2)

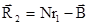. (1.7.5)

Так как векторы 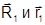коллинеарны, то их векторное произведение

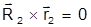. (1.7.6)

С учетом (1.7.5) выражение (1.7.6) можно представить в виде

;

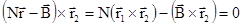или

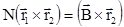. (1.7.7)

Выражение (1.7.7) можно представить в виде

;

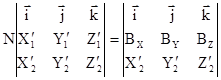или

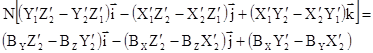; (1.7.8)

где

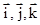- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;

B_X, B_Y, B_Z, X₁’, Y₁’, Z₁’, X₁’, Y₁’, Z₁’ – координаты векторов 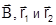в системе координат объекта OXYZ.

;

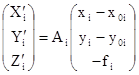где i – номер снимка, а

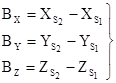(1.7.9)

Так как векторы 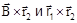коллинеарные (потому что векторы 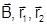компланарны), значение N можно найти как отношение их модулей, то есть

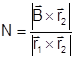; (1.7.10)

В координатной форме выражение (1.7.10) с учетом (1.7.8) имеет вид

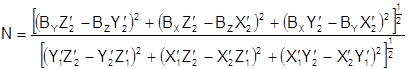; (1.7.11)

У коллинеарных векторов отношение их координат равно отношению их модулей, поэтому можно записать, что:

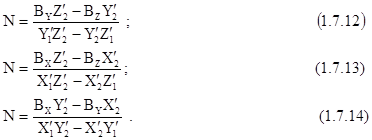
Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках координаты сооветственных точек x₁,y₁ и x₂,y₂, то сначала надо определить по одной из формул (1.7.12)-(1.7.14) значение скаляра N, а затем по формуле (1.7.4) вычислить координаты точки местности X,Y,Z.