Метод Дельфы

Одним из наиболее перспективных методов формирования групповой оценки экспертов является метод Дельфы. Метод представляет собой ряд последовательно осуществляемых процедур, направленных на формирование группового мнения по проблемам, по которым ощущается недостаток информации.

В основу метода Дельфы положены следующие предпосылки:

1) поставленные вопросы должны допускать возможность выражения ответа в виде числа;

2) эксперты должны располагать достаточной информацией для того, чтобы дать оценку;

3) ответ на каждый вопрос (оценка) должен быть обоснован экспертом.

Использование метод Дельфы при подготовке научно - технических прогнозов. При обработке результатов опроса на каждом туре полученные экспертные оценки Kj(i = 1,п) упорядочиваются, например, в порядке убывания и определяются характеристики положения и разброса. При этом в связи с тем, что обычно используют незначительное число экспертов, вместо традиционных числовых характеристик в виде математического ожидания и среднеквадратического отклонения предпочтительно в качестве характеристик положения и разброса использовать более устойчивые—медиану и квартили.

Медиана служит характеристикой группового ответа, предпочтительный интервал квартилей — показателем разброса индивидуальных оценок. За медиану Me принимается член ряда, по отношению к которому число экспертных оценок с начала и с конца ряда (справа и слева от медианного значения) будет одинаковым. Затем определяются верхний и нижний квартили, представляющие собой интервалы, в каждый из которых попадает 25 % значений ряда. Средние квартили, расположенные слева и справа от медианы, считаются предпочтительными как характеристики разброса (Qн —Qв).

На следующем туре каждому эксперту сообщаются значения полученных характеристик. Экспертов, чьи оценки оказались в крайних квартилях, просят обосновать их мнения и причины расхождения с групповым мнением. Так как ответы экспертов анонимны, они имеют возможность пересмотреть свои мнения, данные на предыдущем туре, и при желании исправить оценки. Такая процедура позволяет всем экспертам принять в расчет обстоятельства, которые они могли случайно пропустить или которыми они пренебрегли в предыдущих турах.

После получения новых оценок определяются новые медиана и квартили. Процедура может повторяться 3–4 раза.

Такая итеративная процедура позволяет после каждого тура эффективно уменьшать разброс индивидуальных экспертных оценок. При этом средняя оценка экспертов, изменивших свое мнение, сдвигаете» по направлению средней оценки группы (медианы), а эксперты, не изменившие свои оценки, дают более точное и строгое их обоснование.

Экспериментально установлено, что при использовании метода Дельфы наличие в группе менее знающих экспертов оказывает более слабое влияние их на групповую оценку, чем при простом усреднении оценок, поскольку итерация помогает этим специалистам улучшить свои оценки за счет использования информации от более компетентных специалистов.

Предположим, что от экспертов получено какое - либо число оценок, например, 11. эти оценки упорядочиваются, например, в порядке убывания. За медиану принимается средний член ряда, по отношению к которому число оценок с начала и с конца ряда будет одинаковым. В нашем примере с 11 оценками медиана будет совпадать с оценкой N6 (рис.1). затем определяются верхний и нижний квартили, то есть интервалы N1Q1 и N11Q3. Величины этих квартилей в первом приближении равны значениям оценок ряда в интервале, равном 25 % от начала и 25 % от конца ряда. Таким образом, медиана и квартили образуют на оси ряда четыре интервала, среди которых два средних Q1Me и Q3Me считаются наиболее предпочтительными.

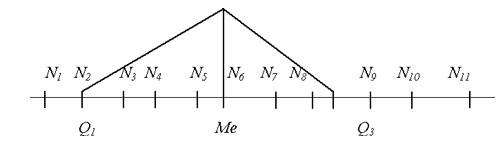
Рис. 1. Медиана и квартили в методе Дельфы

Полученные таким образом показатели принимаются за характеристики распределения оценок: медиана служит характеристикой группового ответа, а предпочтительный интервал квартилей - показателем разброса индивидуальных оценок. Сам прогноз состоит из перечня событий с соответствующими медианами и квартилями дат.