Теоретическое введение. Колебательные процессы (осцилляции) в электрических контурах имеют аналоги в механике

Колебательные процессы (осцилляции) в электрических контурах имеют аналоги в механике. Поведение простейшего осциллятора – математического маятника, представляющего собой небольшое тело, подвешенное на длинном стержне, хорошо изучено: это гармонические колебания с частотой ω₀.

Существенно более сложными являются колебания системы двух одинаковых маятников, связанных между собой слабой пружиной, как это показано на рис. 10.1. Маятники будут участвовать в коллективных колебаниях, вид которых зависит от мгновенной разности фаз смещений маятников (относительная фаза).

Если оба маятника вначале, при t=0,одинаково сместить в одну и ту же сторону (рис.10.1,а), то они будут колебаться как единое целое с постоянной амплитудой и частотой, равными амплитуде и частоте колебаний одиночного маятника ω₀. Наличие пружины никак не повлияет на маятники, поскольку она останется недеформированной. Если при t=0 имеются равные амплитуды и противоположные фазы (маятники сместили из положения равновесия в противоположные стороны на одинаковые углы, рис.10.1,б), то маятники будут колебаться с постоянной амплитудой и с частотой ω₁, слегка повышенной по отношению к ω₀. Эти два вида движения называются нормальными модами колебаний системы связанных осцилляторов, причем вид колебаний с частотой ω₀ называют четной модой нормальных колебаний и обозначают значком «+» (ω⁺=ω₀), а вид колебаний с повышенной частотой ω₁ называют нечетной модой нормальных колебаний и обозначают значком «–» (ω^–=ω₁). Нормальная мода колебаний – это коллективное колебание, при котором амплитуда колебаний каждой движущейся частицы системы остается неизменной.

В более сложных случаях, когда при t=0 имеется относительный сдвиг фаз, результирующее движение можно рассматривать как комбинацию (суперпозицию) двух нормальных мод колебаний. В результате такой суперпозиции (сложения) двух колебаний с разными частотами появляется амплитудно-модулированное сложное колебание. С такими колебаниями приходится встречаться в самых разнообразных явлениях. Примером могут служить не только маятники, но и два звучащих камертона с разными собственными частотами, причем наиболее интересным образом проявляются коллективные колебания, когда частоты колебаний камертонов мало отличаются друг от друга. В этом случае человеческое ухо воспринимает результирующее колебание как гармоническое колебание с переменной амплитудой (амплитудно-модулироаванный сигнал), то есть ухо слышит звук, интенсивность которого периодически меняется с частотой 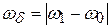(частота биений) и периодом 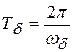. Такой вид суперпозиции гармонических колебаний (при ω₀≈ω₁, но ω₁>ω₀) иллюстрирует рис. 10.2. Само это явление называется биениями, а величины Т_δ и ω_δ – периодом и частотой биений соответственно.

В системе двух связанных слабой пружиной маятников биения могут установиться, если сместить один из них (например, маятник 1, рис. 10.1), удерживая первый на месте, а затем отпустить их одновременно. В этом случае маятник 1 начинает колебаться один (рис.10.2, t=0). С течением времени колебания маятника 2 будут нарастать, а колебания маятника 1 – затухать. Через некоторое время маятник 2 испытывает сильные колебания, а маятник 1 останавливается (рис.10.2, t=t₁). Затем процесс происходит в обратном порядке: колебания маятника 1 нарастают, маятника 2 – затухают (рис.10.2, t=t₂).

В случае четной моды нормальных колебаний маятники движутся вместе, пружина не растянута и частота такая же, как у одиночного маятника. В случае нечетной моды колебаний пружина деформируется, что увеличивает частоту этой моды колебаний. Если в какой-то момент времени смещён только один из маятников, то возникают две нормальные моды колебаний, находящиеся в определенной относительной фазе. Но поскольку частота нечетного колебания немного выше частоты четного колебания, относительная фаза медленно изменяется в процессе коллективного колебания. Амплитуда колебаний первого маятника оказывается равной нулю, а амплитуда второго достигает максимума, когда два нормальных вида колебаний окажутся в противофазе, затем начнется увеличение амплитуды первого маятника и т.д.

Поведение связанных осцилляторов можно легко объяснить с энергетической точки зрения. При t=0 вся энергия сосредоточена в маятнике 1. В результате связи через пружину энергия постепенно передается от маятника 1 к маятнику 2 до тех пор, пока вся энергия не окажется в маятнике 2. Затем, конечно, если система осцилляторов подпитывается извне энергией для компенсации затухания колебаний из-за трения, процесс обмена энергией повторяется от маятника 2 к маятнику 1 и т.д. Таким образом, “биения” – процесс обмена энергией между двумя гармоническими осцилляторами, собственные частоты которых различаются мало, а при t=0 наблюдается относительный сдвиг фаз .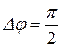

Биения можно наблюдать и в электрической схеме – в двух одинаковых LC – контурах, связанных между собой слабой емкостной связью С_в – аналогом механической связи в виде пружины. Колебания в контурах возбуждаются с помощью преобразователя импульсов (ПИ) – см. рис. 10.3.