Понятие и показатели вариации.

Вариация признака - это различие индивидуальных значений признака внутри изучаемой совокупности.

Вариация возникает в результате того, что индивидуальные значения складываются под влиянием разнообразных факторов. Исследование вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков. По степени вариации можно судить об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками разных явлений.

Именно вариация предопределяет необходимость статистики.

Вариация существует в пространстве и во времени. Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям. Подвариацией во времени подразумевается изменение значений признака в различные периоды (или моменты) времени.

Показатели вариации делятся на две группы: абсолютные и относительные. Самым простым абсолютным показателем является размах вариации. Размах показывает, насколько велико различие между единицами совокупности, имеющимися самое маленькое и самое большое значение признака. Его рассчитывают как разность между наибольшим ( 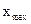) и наименьшим ( 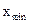) значениями варьирующего признака, т.е.

R=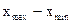

Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику, в качестве такой величины применяют среднюю величину. Средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. При обобщении этих колебаний необходимо вновь прибегнуть к методу средних величин- найти среднюю величину этих отклонений.

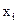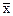Такая средняя называется средним линейным отклонением (`d). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант и ( взвешенная или простая в зависимости от исходных условий) по следующим формулам:

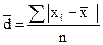(простое)

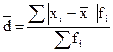(взвешенное)

Среднее линейное отклонение имеет ту же размерность, что и признак.

Если 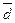имеет большое значение по сравнению с 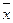, т.е. большое отклонение от 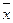, то это свидетельствует о том, что данная совокупность в отношении данного признака неоднородна, а средняя нетипична.

Среднее линейное отклонение применяют довольно редко, т.к. этот показатель не улавливает степень рассеивания признака.

В статистическом исследовании чаще всего применяют показатели дисперсии и среднее квадратическое отклонение.

Дисперсияпредставляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсией (в зависимости от исходных данных ):

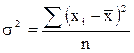( простая)

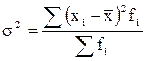( взвешенная)

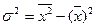
Среднее квадратическое отклонение равно корню квадратному из дисперсии:

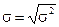
Среднее квадратическое отклонение – это обобщаяющая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак.

Между средним линейным и средним квадратическим отклонениями существует следующее примерное соотношение 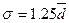, если распределение близко к нормальному.

Для целей сравнения колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в разных совокупностях вычисляются относительные показатели вариации.

Базой для сравнения служит средняя арифметическая. Эти показатели чаще всего выражаются в % и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Различают следующие относительные показатели вариации:

Коэффициент осцилляции ( ):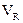

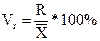
отражает относительную колеблемость крайних значений признака

Линейный коэффициент вариации ( ):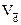

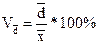
характеризует долю усредненного значения абсолютных отклонений от средней величины.

Коэффициент вариации ( ):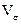

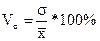
Совокупность считается однородной, если коэффициент вариации не превышает 33%.