Структурные средние величины.

Наряду с рассмотренными средними величинами в качестве статистических характеристик вариационных рядов распределения рассчитываются структурные средние – мода и медиана.

Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.

Медианой называют значение признака, приходящееся на середину упорядоченной (ранжированной) совокупности.

В интервальном ряду для определения моды и медианы используют следующие формулы:

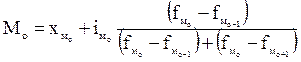
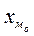- нижняя граница модального интервала

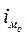- величина модального интервала

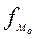- частота модального интервала

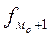- частота следующая за модальным интервалом

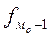- частота предшествующая модальному интервалу

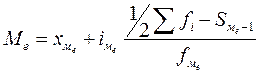
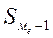- накопленная частота интервала предшествующая медианному интервалу

Медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот.

Пример.

Имеются данные о распределении работников предприятия по уровню среднемесячной заработной платы:

Определить модальный размер и медианный интервал заработной платы.

Решение:Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число работников (70 человек) имеют заработную плату в интервале 700-80о ден.ед., который и является модальным.

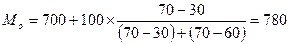ден.ед.

Модальный доход показывает, что большинство работников получали заработную плату в размере 780 ден.ед.

Определяем медианный интервал, в котором находится порядковый номер медианы. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (200/2=100).

В графе «сумма накопленных частот» значение 110 соответствует интервалу 700-800. Это и есть медианный интервал, в котором находится медиана.

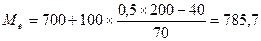ден.ед.

Из расчета видно, что половина работников предприятия имеют заработную плату до 785,7 ден.ед., а половина – выше этой суммы.