И определение процентилей
При исследовании проб на загрязнение объектов окружающей среды, также как и при исследовании заболеваемости населения, сопоставлении показателей с помощью статистических методов часто используют вариационные ряды.
Совокупность некоторых данных состоит из отдельных данных – единиц изучаемой совокупности. Единицы изучаемой совокупности обладают интересующим нас признаком в разной мере. Для каждой единицы совокупности данный признак принимает различные значения, т.е. имеет некоторую вариацию (Теория статистики, 2000).
Вариацией признака называется наличие различий в численных значениях признаков у отдельных единиц совокупности.
Для выявления характера распределения единиц совокупности по варьирующим признакам, определения закономерностей этого распределения, строят ряды распределения единиц совокупностей по какому-либо варьирующему признаку.
Ряды распределения, построенные по количественному признаку, называются вариационными.
Вариационные ряды по способу построения бывают двух видов: дискретные и интервальные.
Дискретный ряд распределения можно рассматривать как такое преобразование ранжированного (упорядоченного) ряда, при котором перечисляются отдельные значения признака и указывается их частота или частость.
По своей конструкции дискретный вариационный ряд состоит из двух столбцов: один столбец – значения варьирующего признака (x – варианты), другой – частоты (m – абсолютное число случаев данного варианта) или частости (w – относительная доля каждой частоты в общей сумме частот).
Для построения вариационного ряда значения признака ранжируют в порядке возрастания или в порядке убывания.
Общая схема вариационного ряда такова: в совокупности, состоящей из N единиц, некоторая переменная величина xi (т.е. какой-то варьирующий признак) принимает различные значения, а каждое из этих значений имеет частоту mi , или частость wi (табл. 2.9).
Таблица 2.9
Общий вид дискретного вариационного ряда
| Вариант xi | Частота mi | Частость wi |
| x1 | m1 | w1 |
| x2 | m2 | w2 |
| . . . | . . . | . . . |
| xn | mn | wn |
| Итого: | 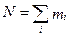
| 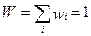
|
Приведённая схема вариационного ряда применяется для тех случаев, когда варьирующий признак принимает небольшое количество значений. Если же вариантов много, то невозможно образовать группы для каждого из них.
Примером дискретного ряда может служить распределение домашних хозяйств по числу членов семьи, представленное в табл. 2.10.
Если число вариантов велико или признак имеет непрерывную вариацию, то объединение отдельных наблюдений в группы производят на базе интервала. Интервал – это такая группа, которая имеет определенные пределы значений варьирующего признака. Эти пределы обозначают двумя числами, которые указывают верхнюю и нижнюю границы интервала. При использовании интервалов образуются интервальные ряды распределения. Строя интервальный вариационный ряд, определяют, прежде всего, число групп, на которое хотят разбить всю совокупность.
Таблица 2.10
Распределение домашних хозяйств России по числу совместно проживающих членов в 1994 году на 1 000 домашних хозяйств (Теория статистики, 2000)
| Число членов домашних хозяйств, чел., xi | Число домашних хозяйств (частота), mi | Число домашних хозяйств (частость), wi |
| 19,2 | ||
| 26,2 | ||
| 22,6 | ||
| 20,5 | ||
| 5 и более | 11,5 | |
| Итого: | 1 000 | 100,0 % |
Для определения числа групп k, на которое можно поделить совокупность, пользуются формулой Стерджесса (Теория статистики, 2000):
k = 1 + 3,322·lg N. (2.37)
Используя формулу Стерджесса можно определить длину интервала h, если отбросить аномальные значения признака и построить ряд с равными интервалами:

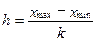 . (2.38)
. (2.38)
При разбиении ряда на интервалы необходимо обращать внимание на значения их границ. Если верхняя граница одного интервала совпадает с нижней границей следующего за ним интервала, то остаётся неясным, в какой интервал попадают пограничные случаи. Пограничное значение можно включить в предыдущие группы или в последующие. Важно соблюдать принятое правило для всего разбиения. Можно также установить границы между группами таким образом, чтобы верхняя граница данного интервала несколько отличалась от нижней границы следующего за ним интервала, например: принимаем значения границ – до 3,0; 3,1 – 5,0; 5,1 – 7,0, 7,1 – 9,0 и т.д.
Любой вариационный ряд можно охарактеризовать с помощью накопленных частот. Накопленная частота показывает число единиц совокупности, у которых значение варианта не больше данного. Накопленная частота для данного варианта или для верхней границы данного интервала получается суммированием (накапливанием) частот всех предшествующих интервалов, включая данный.
Если вместо абсолютных частот использовать частости, то аналогично получим накопленные частости. Ряд частостей применяют, когда совокупность очень велика. Кроме того, они позволяют сравнивать распределения по одному и тому же признаку в разных по численности совокупностях. Для приведения частостей, относящихся к интервалам разной длины, к сопоставимому виду, используют относительную плотность распределения. Вычисляют абсолютную и относительную плотности распределения.
Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала – 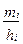 .
.
Относительная плотность распределения – это частость, приходящаяся на единицу длины интервала – 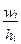 .
.
Для характеристики распределения применяют средние величины, такие как средняя арифметическая простая, средняя арифметическая взвешенная, мода, медиана.
Среднюю 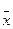 арифметическую простую определяют по формуле:
арифметическую простую определяют по формуле:
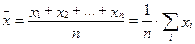 , (2.39)
, (2.39)
где xi – текущие величины признака, n – число признаков в вариационном ряду.
Среднюю 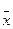 арифметическую взвешенную определяют по формуле:
арифметическую взвешенную определяют по формуле:
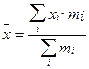 . (2.40)
. (2.40)
В отличие от средней арифметической, на которую оказывают влияние все
значения xi , значение медианы совершенно не зависит от крайних значений признака.
Медианой называют такое значение признака, которое приходится на середину ранжированного ряда. Таким, образом, в ранжированном ряду распределения одна половина признака имеет значения признака, превышающие медиану, другая – меньше медианы.
Значение медианы Me при использовании частот на данном интервале определяют по следующей формуле:
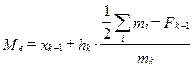 , (2.41)
, (2.41)
где xk-1 – нижняя граница медианного интервала; hk – длина медианного интервала; Fk-1 – накопленная частота интервала, предшествующего медианному; mk – частота медианного интервала.
Если вместо частот использовать частости, то значение медианы определяют по формуле:
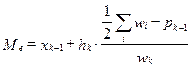 , (2.42)
, (2.42)
где pk-1 – накопленная частость интервала, предшествующего медианному; wk – частость медианного интервала.
Для анализа структуры вариационного ряда используют такие значения признака, которые делят все распределение на равные группы, называемые квантилями. Квартили, квинтили, децили и процентили являются частными случаями квантилей.
Медиана делит вариационный ряд пополам: 50 % его признаков меньше медианы и 50% – больше. Таким образом, медиана является 50-м процентилем.
Квартилями называются такие значения признака, которые делят распределение на четыре равные части.
Квинтили делят распределение на пять равных частей.
Децили делят распределение на десять равных частей или, что то же самое, децили соответствуют десятые части совокупности.
Процентили делят распределение на сто равных частей. Или другими словами, процентили – это величины, делящие выборку данных  на 100 групп, содержащих (по возможности) равное количество наблюдений, по 1 % наблюдений в каждой группе.
на 100 групп, содержащих (по возможности) равное количество наблюдений, по 1 % наблюдений в каждой группе.
Можно еще сказать, что процентили это значения в ряду наблюдений в порядке возрастания (убывания) величин, которые делят распределение на 100 равных частей.
Квартили, квинтили, децили и процентили определяют по тем же формулам, что и медиану.
При исследовании проб на загрязнение объектов окружающей среды часто встречается необходимость определить число проб, превышающих 95 % всех исследованных проб. Для этого определяют 95-й процентиль.
95-му процентилю – соответствует уровень загрязнения пробы, превышающий по этому показателю 95 % всех исследованных проб.
Пример 4. На некоторой территории проведено обследование вод хозяйственно-бытового назначения. В обследованных источниках обнаружено присутствие свинца. Всего взято 50 проб. ПДК для свинца в водах хозяйственно бытового назначения составляет 0,1 мг/кг. В проведённых анализах обнаружены концентрации свинца, значения которых приведены в табл. 2.11. Для построения вариационного ряда значения концентраций ранжированы в порядке их возрастания.
В соответствии с принятой оценкой степени напряжённости медико-экологической ситуации (см. табл. 3.37) степень напряжённости оценивают по величине превышения концентрации вредного вещества 1-го класса опасности над ПДК в следующих значениях: до 1; 1,1 – 2,0; 2,1 – 3,0; 3,1 – 5,0 и более 5,0.
Разбить вариационный ряд на интервалы в соответствии со степенью напряжённости. Определить число проб в каждой группе. Определить частость. Определить накопленные частоты и частость. Определить значение медианы. Определить значение 95-й процентили. Сделать выводы о пригодности обследованного источника для использования воды в хозяйственно-бытовых целях.
Таблица 2.11
Результаты анализа образцов воды на содержание свинца
| № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг |
| 0,17 | 0,23 | 0,34 | 1.28 | ||||||
| 0,17 | 0,23. | 0,41 | 1,39 | ||||||
| 0,18 | 0,24 | 0,44 | 1,62 | ||||||
| 0,19 | 0,24 | 0,47 | 1,80 | ||||||
| 0,05 | 0,21 | 0,24 | 0,48 | 2,19 | |||||
| 0,05 | 0,21 | 0,25 | 0,70 | 2,21 | |||||
| 0,1 | 0,21 | 0,28 | 0,74 | 2,41 | |||||
| 0,1 | 0,21 | 0,30 | 0,76 | 2,63 | |||||
| 0,1 | 0,22 | 0,31 | 0,77 | 2,76 | |||||
| 0,1 | 0,22 | 0,32 | 0,80 | 27,80 |
Разобьём вариационный ряд на 5 интервалов в соответствии с уровнями превышения. Результаты поместим в табл. 2.12.
95-ю процентиль определим, используя формулу (3.46), отбросив при этом последнее 50-е значение ряда, как «аномальное».
В нашем примере вариационный ряд содержит 50 проб.
95-й уровень = 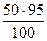 = 47,5.
= 47,5.
Таблица 2.12
Группировка загрязнения воды по величине превышения
концентрации свинца над ПДК
| Величина превышения концентраций | Количество анализов | Середина интервала, xi | Накопленные | Плотность распределения в интервале,
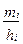
| ||
| Единиц mi | % или частость, wi | Частоты, Fi | Частости, pi | |||
| От 0 до 1,0 | 0,5 | |||||
| 1,1-2,0 | 1,55 | 8,89 | ||||
| 2,1-3,0 | 2,55 | 31,1 | ||||
| 3,1-5,0 | 4,05 | 7,36 | ||||
| > 5,0 | – | – | ||||
| Итого: | – | – |
Полученное число округляем до целого, таким образом 47-я проба будет нижней границей 95-го процентиля. Величина 95-го процентиля будет:
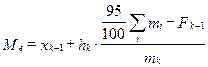 = 2,41 + 0,35
= 2,41 + 0,35 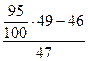 = 2,421.
= 2,421.
Характеристиками вариационного ряда являются: являются дисперсия и среднее квадратическое отклонение.
Дисперсию называют мерой вариации вариационного ряда. Дисперсию для не сгруппированного ряда вычисляют по формуле:
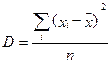 . (2.43)
. (2.43)
Для сгруппированного ряда дисперсию вычисляют по формуле:
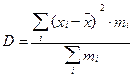 . (2.44)
. (2.44)
Среднее квадратическое отклонение измеряется в тех же единицах, что и варьируемый признак, и исчисляется путём извлечения квадратного корня из дисперсии:
для несгруппированных данных:
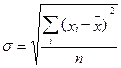 . (2.45)
. (2.45)
для сгруппированных данных:
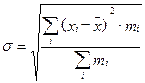 . (2.46)
. (2.46)
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Отклонение, выраженное в σ, называется нормированным или стандартизованным.
Дата добавления: 2015-10-06; просмотров: 2064;
