Оценка достоверности изучаемых показателей
Выше уже говорилось о необходимости подтверждения причинных связей между воздействием и эффектами на здоровье человека.
Целью изучения влияния антропогенных факторов на здоровье является установление взаимосвязей между факторами, действующими на данной территории или в данном населённом пункте и заболеваемостью населения.
Для достижения этой цели необходимо решить следующие задачи:
1 – количественно охарактеризовать состояние окружающей среды на обследуемой территории;
2 – изучить и количественно охарактеризовать состояние здоровья населения на данной территории;
3 – выявить характер и степень взаимосвязи между факторами окружающей среды и состоянием здоровья населения;
4 – разработать практические рекомендации по уменьшению или ликвидации вредных факторов.
Как уже было сказано раньше, при таких исследованиях необходимо иметь как минимум две группы населения – подверженных и не подверженных действию изучаемых вредных факторов.
Из этого следует, что для изучения необходимо сравнивать состояние здоровья населения на двух территориях – опытной и контрольной. Эти территории должны отличаться по характеру и степени, либо только по степени загрязнения окружающей среды. В то же самое время, выбранные территории не должны различаться по обеспеченности медицинской помощью, уровню её специализации и организации. В качестве контрольной может быть также выбрана территория, на которой изучаемые факторы находятся в пределах допустимых уровней.
Численность наблюдаемых групп может охватывать 20 – 25 тыс. человек, что примерно соответствует количеству населения обслуживаемого одной поликлиникой.
В первую очередь исследуются отчётные статистические материалы, имеющиеся в лечебных учреждениях. Как мы видели, в таких материалах содержатся сведения об ограниченном количестве заболеваний. Изучение медицинских карт может дать информацию о заболеваниях не входящих в отчётность. При необходимости, как уже говорилось ранее, проводятся дополнительные медицинские обследования всего населения или отдельных групп.
Для описания причинных связей между воздействием и эффектами на здоровье человека используют непрерывные случайные величины. Непрерывными называют величины, которые могут принимать любое значение на некотором интервале. К непрерывным случайным величинам относятся и характеристики факторов воздействия (концентрация загрязнителя на определённой территории, накопленная доза в отдельных организмах популяции и т.д.) и показатели здоровья населения (заболеваемость, смертность и т.д.).
Известны различные функции распределения непрерывных случайных величин: нормальное (гауссово) распределение, экспоненциальное распределение, распределения Вейбулла, Гомперца и Гомперца-Мейкема, распределение Стьюдента (t-распределение, распределение Фишера (F-распределение) и другие.
Нормальное распределение играет особо важную роль при решении прикладных задач во всех естественных науках: медицине, биологии, физике, химии и т.д. Практическая значимость этого распределения при оценке экологических рисков объясняется тем, что показатели здоровья населения на популяционном уровне, показатели заболеваемости и другие подчиняются распределению Гаусса.
Распределение Гаусса, называемое также нормальным распределением, описывается формулой (2.27):

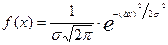 , (2.27)
, (2.27)
где случайная величина x принимает любые значения в диапазоне - 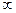 <x<
<x< 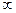 ,
,
Δx= 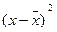 . Значение
. Значение 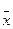 соответствует точке симметрии распределения, а дисперсия D=σ2 (см. рис. 2.1).
соответствует точке симметрии распределения, а дисперсия D=σ2 (см. рис. 2.1).
Согласно распределению Гаусса вероятность событий:
P(|x- 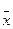 |)
|)  σ равна
σ равна
P(|x- 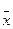 |
|  σ)=
σ)= 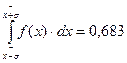 . (2.28)
. (2.28)
Соответственно:
P(|x- 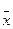 |
|  2σ)= 0,954, (2.29)
2σ)= 0,954, (2.29)
P(|x- 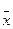 |
|  3σ)= 0,9974. (2.30)
3σ)= 0,9974. (2.30)
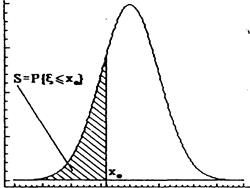
На рис. 2.1. приведена зависимость для плотности распределения непрерывной случайной величины.
| f(x) | |
| 0,4 0,3 0,2 0,1 |
|
 - 4 -3 -2 -1 0 1 2 3 4 x - 4 -3 -2 -1 0 1 2 3 4 x
| |
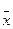
|
Рис. 2.1. Распределение Гаусса
Геометрически величина σ совпадает с расстоянием от 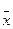 до точек перегиба кривой f(x) Гаусса, т.е. в точках x=
до точек перегиба кривой f(x) Гаусса, т.е. в точках x= 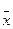 ±σ функция плотности имеет точки перегиба, в которых кривая меняется с выпуклой на вогнутую.
±σ функция плотности имеет точки перегиба, в которых кривая меняется с выпуклой на вогнутую.
Графическая интерпретация связи между этими величинами имеет тот смысл, что для распределения Гаусса не зависимо от значений параметров 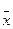 и σ площадь под кривой составляет:
и σ площадь под кривой составляет:
| 0,68 | для интервала | 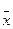 ±σ; ±σ;
|
| 0,95 | для интервала | 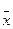 ±1,96σ; ±1,96σ;
|
| 0,99 | для интервала | 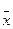 ±2,58σ; ±2,58σ;
|
| 0,9974 | для интервала | 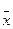 ±3σ. ±3σ.
|
Широкое применение распределения Гаусса на практике объясняется тем фактом, что при нормальном распределении случайных величин, вероятность попадания значений за пределы довольно узкого интервала, с границами 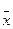 ±3σ, составляет всего 0,0026, т.е. менее 0,3 %.
±3σ, составляет всего 0,0026, т.е. менее 0,3 %.
Использование распределения Гаусса и его свойств позволяет обрабатывать результаты санитарно-экологических наблюдений и за состоянием здоровья населения и за состоянием окружающей среды, определять степень их взаимосвязи и оценивать достоверность полученных результатов.
На основе полученных данных в соответствии с формулами 2.1 – 2.26, приведёнными в разделе 2.1.3.1 «Расчёт показателей заболеваемости взрослого населения», производится расчёт тех показателей, для расчёта которых имеются соответствующие данные, например: суммарный показатель заболеваемости, доля (удельный вес) различных форм и групп болезней и структура заболеваемости, число детей с врождёнными аномалиями, число посещений по поводу заболеваний и др.
Итак, мы вычислили ряд показателей. Теперь надо убедиться, что они не случайны и отражают реальную картину состояния заболеваемости, другими словами, надо убедиться в их достоверности. Оценка достоверности полученных показателей осуществляется с использованием методов статистической обработки.
Для любого полученного показателя, прежде всего, необходимо вычислить стандартную среднюю ошибку. Стандартную среднюю ошибку m вычисляют по формуле (2.31):
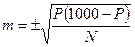 , (2.31)
, (2.31)
где m –величина стандартной средней ошибки; P– показатель заболеваемости; N – число наблюдений.
Следует обратить внимание на то, что формула (2.31) справедлива только для значений P<1 000.
Если величина утроенной стандартной средней ошибки превышает величину показателя заболеваемости, то такой показатель считают статистически не достоверным и он исключается из дальнейшей обработки.
Для оценки достоверности различия сравниваемых показателей заболеваемости по выбранным территориям или когортами используют критерий Стьюдента-Фишера.
При использовании этого критерия оценка достоверности производится по формуле (2.32):
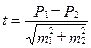 , (2.32)
, (2.32)
где: t – коэффициент достоверности; P1 и P2 – показатели заболеваемости в первой и второй когортах; m1 и m2 – стандартная средняя ошибка в первой и второй когортах.
В табл. 2.6 приведены значения коэффициентов достоверности и доверительного интервала. Значения коэффициента достоверности t сравнивают с табличным значением (табл. 2.6).
В большинстве случаев в медицинской практике, также как и в практике биологических и экологических исследований считают результаты приемлемо точными, если они попадают в доверительный интервал 0,95. Это означает, что истинное значение изучаемого параметра с вероятностью 95 % находится в его пределах.
Таблица 2.6
Значения коэффициента достоверности
| Коэффициент достоверности t | 1,28 | 1,65 | 1,96 | 2,58 | 3,03 | |
| Доверительный интервал, α | 0,68 | 0,8 | 0,9 | 0,95 | 0,99 | 0,999 |
| Доверительная вероятность, p | 0,32 | 0,20 | 0,10 | 0,05 | 0,01 | 0,001 |
Пример 1. На территории «А» с повышенным загрязнением атмосферного воздуха в течение 1 года диагностировано заболевание бронхиальной астмой у 1 527 мужчин, при общей численности мужского населения 8 760 человек. На контрольной территории «В» расположенной в зелёной зоне число мужчин, заболевших астмой в течение того же года составило 518, при численности мужского населения 7 780 человек. Необходимо определить суммарные показатели заболеваемости для территории «А» и зоны «В», оценить достоверность данных по каждой зоне и достоверность различия полученных показателей.
Показатель суммарной заболеваемости мужчин на территории «А» в соответствии с формулой (2.7):
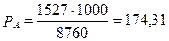 на 1 000 мужчин.
на 1 000 мужчин.
Стандартная средняя ошибка для территории «А» в соответствии с формулой (2.31):
mA= 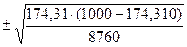 =3,72
=3,72
Показатель суммарной заболеваемости мужчин на территории «А» в соответствии с формулой (2.7):
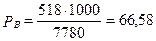 на 1000 мужчин.
на 1000 мужчин.
Стандартная средняя ошибка для территории «А» в соответствии с формулой (2.31):
mB = 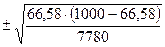 =2,82.
=2,82.
Утроенное значение стандартной средней ошибки не превышает показателя заболеваемости ни в первом, ни во втором случаях, так что данные по заболеваемости можно считать достоверными.
Достоверность различия сравниваемых показателей заболеваемости по выбранным территориям проверяем с помощью критерия Стьюдента-Фишера, используя формулу (2.32):
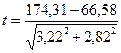 = 25,17.
= 25,17.
Величина коэффициента достоверности намного превышает значения, приведённые в табл. 2.6, что подтверждает различие между показателями заболеваемости на сравниваемых территориях.
Часто возникает вопрос о том, какое минимальное число наблюдений (случаев заболевания, больных пациентов и т.п.) необходимо иметь, чтобы получить оценку с допустимой точностью, например, с ошибкой ±5 % или ±10 %. Чаще всего требуется определить показатели с ошибкой ±5 %.
Предельную ошибку показателя определяют по формуле (2.33):
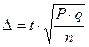 , (2.33)
, (2.33)
где Δ – ошибка показателя; t – коэффициент достоверности; P –величина показателя в % или относительных единицах; q=(1-P) или q=(100-P) в зависимости от того, в каких величинах определён показатель; n – число наблюдений.
Чтобы получить результат с 95 %-м доверительным интервалом (см. табл. 2.6), коэффициент достоверности t принимают равным 2.
Тогда из формулы (2.33) можно найти величину числа n наблюдений (2.34):
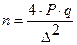 . (2.34)
. (2.34)
Пример 2. По данным медицинского пункта школы в течение года за медицинской помощью обратились 90 % учеников. Какова должна быть минимальная численность группы наблюдения, чтобы оценка заболеваемости имела ошибку ±5 %?
В соответствии с формулой (3.36) получим:
n= 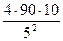 = 144.
= 144.
Т.е., для получения показателя о заболеваемости с погрешностью ±5 % необходимо иметь группу учащихся не менее 144 человек.
Если численность населения, проживающего на изучаемой территории известна, то для расчёта необходимого числа наблюдений используют формулу (2.35):
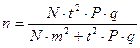 . (2.35)
. (2.35)
2.2.4.2. Расчёт стандартизованных показателей
Существенное влияние на уровень и структуру заболеваний оказывают не только факторы окружающей среды, но и состав населения: возраст, пол, группы повышенного риска, к которым обычно относят стариков, детей и беременных женщин. При сопоставлении заболеваемости по наблюдаемым территориям для исключения влияния структуры населения применяют метод стандартизации. Стандартизованные показатели, рассчитанные по данному методу, показывают, какими были бы показатели заболеваемости сравниваемых групп, если бы они имели одинаковый возрастной и половой состав.
Расчёт стандартизованных коэффициентов рассмотрим на простом примере.
Пример 3.Сравнить показатели заболеваемости по физическим недостаткам (искривление позвоночника, плоскостопие, и др.) учащихся двух школ. Данные о численности учащихся по возрастным группам в школе «А» и в школе «В» приведены в таблицах 2.7 и 2.8.
Таблица 2.7
Данные по школе «А»
| Возрастная группа, лет | Число учащихся, чел. | Число заболеваний физич. недостатками | Заболеваемость (число учащихся с физич. откл) на 1000 | Стандарт, человек | Ожидаемое число больных в группе стандарта |
| 6 – 14 | |||||
| 15 – 19 | 77,52 | ||||
| Всего: | 251,94 |
Распространённость заболеваний среди детей (заболеваемость) рассчитываем на
1 000 детей в соответствии с формулой (2.11). Данные расчёта помещаем в 4-м столбце.
Таблица 2.8
Данные по школе «В»
| Возрастная группа, лет | Число учащихся, чел. | Число заболеваний физич. недостатками | Заболеваемость (число учащихся с физич. откл) на 1000 | Стандарт, человек | Ожидаемое число больных в группе стандарта |
| 6 – 14 | 64,29 | 109,29 | |||
| 15 – 19 | 112,5 | 57,37 | |||
| Всего: | 73,77 | 154,91 |
За стандарт можно принять общую численность населения двух исследуемых групп или численность населения одной из изучаемых групп данного возрастного состава, или численность населения какой-либо третьей группы.
Мы принимаем за стандарт суммарную численность учащихся обеих школ и данные по численности стандарта помещаем в пятом столбце.
Далее составляется простая пропорция: в школе «А» в возрастной группе 6 – 14 лет заболеваемость составляет 64,26 на 100 человек. Сколько было бы больных в этой возрастной группе при численности учащихся равной стандарту 1700 человек:
1000 – 4,29
1700 – х (2.36)
откуда 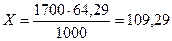 .
.
По аналогии рассчитываем стандартизованные показатели для других возрастных групп и для всех учащихся по обеим школам и помещаем данные в шестом столбце.
Сравнивая ожидаемые числа больных в группах стандарта, обнаруживаем, что в школе «В» заболеваемость учащихся была бы гораздо меньше по сравнению со школой «А».
При анализе когорт населения, проживающих на разных территориях, можно разбить всё население на такие возрастные категории, в которых заболеваемость примерно одинакова, например: 15 – 19 лет, 20 – 29, 30 – 39, 40 – 49, 50 – 59, 60 лет и старше.
Дата добавления: 2015-10-06; просмотров: 4003;
