Свойства непрерывных функций

Свойства функций, непрерывных в точке:

1. Если функции f₁(х) и f₂(х) непрерывны в точке х₀, то их сумма
f₁(х) + f₂(х), произведение f₁(х)*f₂(х) и частное f₁(х)/f₂(х) (при условии
f₂(х) ¹ 0) также являются функциями, непрерывными в точке х₀.

Это следует из определения непрерывности и свойств пределов функций.

2. Если функция у = f(х) > 0 непрерывна в точке х₀ и f(х₀) > 0, то существует такая окрестность точки x₀, в которой f(х) > 0.

В самом деле, при малых приращениях аргумента в соответствии со вторым определением непрерывности можно получить сколь угодно малое приращение функции, так что знак функции в окрестности точки не изменится.

3. Если функция y = f(u) непрерывна в точке u₀ , а функция u = j(х)

непрерывна в точке u₀ = j(х₀), то сложная функция y = f([(j(х)] непрерывна в точке х₀: 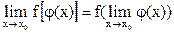. Иными словами, под знаком сложной функции можно переходить к пределу.

Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны на любом промежутке из области их определения.

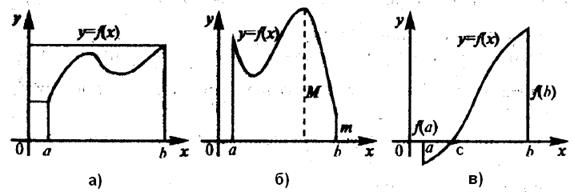
На рисунке 9.12 представлены графики функций, непрерывных на отрезке [a; b].

Свойства функций, непрерывных на отрезке:

1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке (см. рисунок 2.12 (а)).

2. Если функция непрерывна на отрезке, то она достигает на нем наименьшего значения и наибольшего значения М (теорема Вейерштрасса) (см. рисунок 2.12 (б), m - наименьшее значение, M - наибольшее значение).

3. Если функция непрерывна на отрезке, и ее значения на концах этого отрезка имеют противоположные знаки, то внутри отрезка найдется точка, в которой значение функции равно нулю (теорема Больцано-Коши) (см. рисунок 2.12 (в), в точке c Î[a; b] f(c) = 0).

[1] Чтобы проиллюстрировать случай, когда предел не существует, можно, например, на рис. 2.4 изменить график функции таким образом, чтобы он бесконечно приближался к вертикальной асимптоте х = х₀ + d или х = х₀ - d.

[2] Происхождение названия теоремы: график функции f₁(х) - траектория движения первого милиционера в участок А, график f₂(х) - траектория движения второго милиционера в тот же участок, а график f(х) - траектория движения пьяного, который, в соответствии с неравенством
f₁(х) £ f(х) £ f₂(х) в любой момент х находится между двумя милиционерами. Тогда и пьяный неизбежно придёт туда же, в участок А.

[3] Можно показать, что любую показательную функцию можно свести к экспоненциальной. Действительно, пусть у = a^x = (e^{ln a})^x = e^{x*ln a} = е^bx , где
b = ln a.