Признаки существования и основные свойства пределов
Рассмотрим признаки существования предела и некоторые свойства пределов (здесь соответствующие теоремы доказываться не будут).
Признаки существования предела[1]
I. Существование предела монотонной ограниченной функции. Если функция монотонна и ограничена, то она имеет предел.
Здесь возможны следующие варианты:
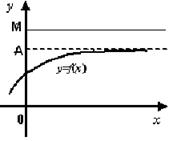
1) Если функция ограничена сверху f(x) £ M, то ее предел А £ M. Причем если она
а) не убывает, то она имеет предел А при x ® х0-0 (слева) и x ® +¥
(см. рис. 2.5)

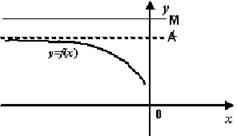
б) не возрастает, то она имеет предел А при x ® х0+0 (справа) и
x ® -¥ (см. рис. 2.6)

2) Если функция ограничена снизу f(x) ≥ M, то ее предел А ≥ M. Причем если она
а) не убывает, то она имеет предел А при x ® х0-0 (справа) и x ® -¥
(см. рис. 2.7)
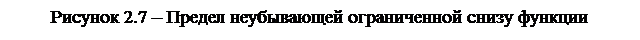
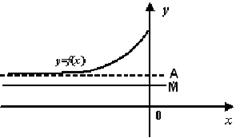
б) не возрастает, то она имеет предел А при x ® х0-0 (слева) и
x ® +¥ (см. рис. 2.8)
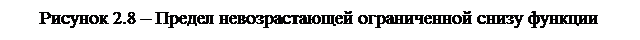
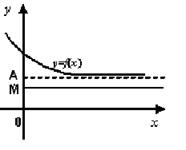
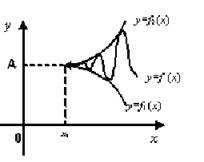
II. Теорема «о двух милиционерах»[2]. Если функция y = f(х) заключена между двумя функциями f1(х) и f2(х), имеющими одинаковый предел, то функция f(х) имеет тот же предел (при той же базе).
Т.е. если f1(х) £ f(х) £ f2(х) и 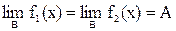 , то
, то 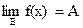 .
.
Дата добавления: 2015-10-06; просмотров: 945;
