Теорія Бора для воднеподібних атомів

В теорії Бора вважається, що рух електрона по стаціонарній орбіті відбувається за законами класичної механіки. Оскільки маса m електрона значно менша від маси ядра атома, можна вважати ядро нерухомим. Розмістимо ядро в початку системи координат.

Запишемо другий закон Ньютона для електрона, який обертається навколо ядра по круговій орбіті радіуса r:

. (3)

Потенціальну енергію електрона на відстані r будемо вважати рівною нулю. При таких умовах повна енергія Е електрона на відстані r від ядра буде дорівнювати

(4)

Рівняння (2), (3), (4) утворюють систему, розв’язавши яку відносно r та Е, можна знайти радіуси стаціонарних орбіт та значення енергії атома у відповідних стаціонарних станах. Для цього, виключаючи швидкість v з (2) та (3), знайдемо радіуси орбіт:

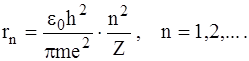(5)

В формулі (5) кожному значенню числа n відповідає певне значення r_n радіуса стаціонарної орбіти.

Для визначення енергії E_n стаціонарних станів атома виключимо v² з рівнянь (3) та (4) і в одержане таким чином співвідношення:

,

підставимо замість r значення r_n з формули (5). Після очевидних перетворень приходимо до виразу:

(6)

Ми одержали дискретний ряд значень енергії – набір енергетичних рівнів атома.

При Z = 1 та n = 1 формули (5) та (6) приводять до значень r₁ та E₁ – радіуса першої, найближчої до ядра, стаціонарної орбіти в атомі водню та енергії атома водню у найнижчому енергетичному стані, який називають основним станом. Величину r₁ = 0,529· 10^–10 м називаютьборівським радіусом,а Е₁–енергієюосновного стану атома водню. Легко бачити, що, використовуючи значення r₁ та E₁, формули (5) та (6) можна подати у вигляді:

В атомній фізиці при вимірюваннях енергії користуються більш зручною, аніж джоуль, позасистемною одиницею – електрон-вольт (1 еВ = 1,6· 10^–19 Дж). В цих одиницях Е₁ = – 13,6 еВ.

Отже, радіуси стаціонарних орбіт, а такоженергетичні рівні атома водню та будь-якого воднеподібного атома легко розраховуються через борівський радіус та енергію основного стану атома водню.

Від’ємні значення енергії стаціонарних станів обумовлені вищезгаданим способом відліку потенціальної енергії електрона в полі ядра.