ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРИ ПОМОЩИ МОСТОВОЙ СХЕМЫ

Одним из наиболее точных методов измерения сопротивлений является мостовой метод, при котором неизвестное измеряемое сопротивление сравнивают с тремя известными. На рис. I показана схема моста постоянного тока. Четыре сопротивления: R₁, R₂, R₃ и R_Х соединены в замкнутый четырехугольник, стороны которого образуют плечи моста. В одну из диагоналей моста включают источник тока, в другую - магнитоэлектрический индикатор высокой чувствительности. Если в цепи прибора тока нет, мост считается уравновешенным. Это может быть только при равенстве потенциалов

в точках C и D т.е. j_C -j_D =0.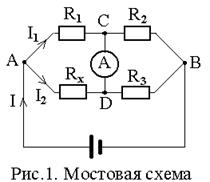

Уравновешивают мост, подбирая сопротивления R₂ или R₃. В уравновешенном мосте произведения сопротивлений противоположных плеч равны: R₁×R₃ =R₂ ×R_Х .

Докажем это соотношение, пользуясь вторым правилом Кирхгофа. Для замкнутых контуров ACDA и CBDC можно записать следующие уравнения (при условии равновесия моста):

I₁ R₁-I₂ R _х=0 и I₁ R₂ - I₂R₃=0.

Решая эту систему уравнений, получим:

R_х= R₁ ( R₃/R₂)

Из этого соотношения видно, что равновесие моста может быть получено двумя способами: при постоянном отношении постоянных сопротивлений R₃/R₂ изменением сопротивления R₁, или при постоянном сопротивлении одного плеча R₁ изменением соотношения сопротивлений двух других плеч R₃/R₂ .

В зависимости от способа получения равновесия моста существуют различные его конструкции. На рис. 2 показана мостовая схема, в которой

равновесие моста достигает­ся вторым способом. Эта схема называется мостом Уитстона.

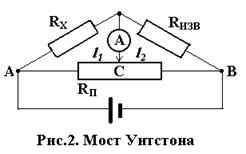
Так как сопротивления плеч потенциометра R_П: R_АC и R_CB пропорциональных их длинам l₁ и l₂, тогда

R_X = R_ИЗВ (l₁/ l₂) (1)

Если длина потенциометра l , то l₂ = l – l₁ и

R_Х = R_ИЗВ(l₁/ (l – l₁)) (2)

Таким образом, процесс измерения сопротивления с помощью моста Уитстона сводится к балансировке моста и измерению длин плеч l₁ и l₂ потенциометра R_П. Последнее может осуществляться с помощью линейки или шкалы, смонтированной на потенциометре.

Точность измерения сопротивлений определяется точностью уравновешенности моста, которая существенно зависит от чувствительности индикатора и величины напряжения питания.

Мостовые схемы образуют обширный класс измерительных цепей, широко используемый в радиотехнике, автоматике и других областях техники.

Описание установки, измерения и обработка результатов измерений

Электрическая схема передней панели лабораторной установки приведена на рис.3.

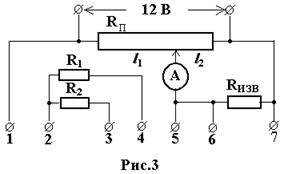
ВНИМАНИЕ! В установке для данной лабораторной работы используется высокоточный круговой потенциометр, который размещен горизонтально на передней панели установки. Его шкала расположена впереди, а ручка вращения сзади. Максимальный угол поворота ручки потенциометра 330⁰. Шкала потенциометра разбита на 33 части (по 10⁰) Внимательно изучите шкалу потенциометра.

Работу выполняют в следующем порядке:

1. С помощью проводов собирают на лабораторном стенде схему моста Уитстона, вклю­чив в нее резистор с неизвестным сопротивлением R₁. Для этого необходимо соединить клеммы I и 2, а также 4 и 5.

2. Подключают источник питания 12 В и балансируют мост, перемещая движок потенциометра до тех пор, пока стрелка индикатора (миллиамперметра А) не установится на отметке "О".

3. Измеряют длины плеч потенциометра и результат заносят в таблицу 1.

ВНИМАНИЕ! При использовании кругового потенциометра длины плеч l₁ и l₂ необходимо представить в угловой мере, как: j₁ и j₂ . В этом случае формулы (1),(2) будут иметь вид:

R_Х = R_ИЗВ (j₁ / j₂) = R_ИЗВ(j₁ / (j_max. – j₁)) (3)

где j_max.=330⁰ , j₁ отсчитывается от 0.

Измерения повторяют не менее 3 раз. При каждом последующем измерении (для снятия второго и следующих отсчетов ) необходимо повернуть ручку переменного резистора (расположен в левом верхнем углу на передней панели лабораторной установки) на угол »10-20⁰, а затем выполнить балансировку моста.

4. В той же последовательности измеряют сопротивление резистора R₂ , а затем сопротивление последовательно и параллельно соединенных резисторов R₁ и R₂

5. Результаты всех измерений и вычислений заносят в таблицу I.

Таблица I

	RИЗВ Ом	j1 град	j2 град	Rx Ом	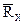Ом	D Rx Ом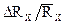
Резистор R1
Резистор R2
Последовательное соединение R1 и R2
Параллельное соединение R1 и R2

6. Погрешность измерений вычисляют по формуле:

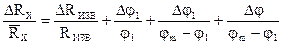(4)

В формуле (4): ∆R_ИЗВ/R_ИЗВ принять равным 5% , Dj=2,5⁰ (половина наименьшего деления шкалы кругового потенциометра).

Формулу (4) можно упростить, полагая j₁=j_m/2 (в этом случае точность измерений наибольшая) и Dj₁=Dj. Сделайте это самостоятельно.

7. Результаты измерений сопротивлений при их последовательном и параллельном соединениях сравнивают с величинами, рассчитанными по известным формулам: R_ПОСЛ=R₁+R₂ и R_ПАРАЛ =(R₁× R₂) /(R₁+R₂).

Вывод записать письменно.

ИЗУЧЕНИЕ ЗАКОНОВ ОМА ДЛЯ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Обобщённый закон Ома.

Рассмотрим участок электрической цепи, изображенный на рис.1.

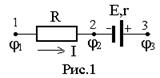
Подчеркнём, что нами выбран участок из некоторой произвольной электрической цепи. В ней могут быть другие ЭДС, не входящие в выделенный участок, под действием которых ток по данному участку может течь и навстречу данной ЭДС Е.

Примечание. 1) На рис.1 вертикальными линиями показано изображение источника тока, имеющего характеристики: ЭДС E и внутреннее сопротивление r. Часто вместо слов источник тока говорят: ЭДС. 2)Терминология: участок цепи, содержащий ЭДС и сопротивление R называется неоднородным, а содержащий только сопротивление R –однородным.

Найдем взаимосвязь между величинами I, Е, j₁, j₂, j₃ для рассматриваемого участка. Обозначим общее сопротивление между точками 1-3 через R₀: R₀=R+r, гдеR-сопротивление внешнего участка цепи, r- внутреннее сопротивление источника ЭДС.

Выразим потенциал точки I через потенциал точки 3.