Силові співвідношення, умови самогальмування і ККД гвинтової пари

Силові співвідношення вивчимо на прикладі прямокутної різьби. Розгля­немо гайку (рис. 5.5, а), що нагвинчується на гвинт рушійною силою F_t, при­кладеною по середньому колу різьби, i навантажену осьовою силою. Прийме­мо умову, що все навантаження, прикладене до гайки, зосереджене в точці. Рух гайки можна представити як переміщення вантажу нагору по похилій площині з кутом підйому y, рівним куту підйому різьби гвинта (рис. 5.5, б). Крім сил F_t і F_a на вантаж діють нормальна реакція площини F_n і сила тертя F_f :

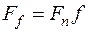, (5.2)
де f – коефіцієнт тертя.

Рис. 5.5. Розрахункова схема до визначення силових співвідношень

у гвинтовій парі

Проектуючи діючі сили на осі x та y, отримуємо (використовуючи умову рівноваги тіла на похилій поверхні)

(5.3)

Розв‘язуючи систему рівнянь (5.3), маємо:

,
звідки:

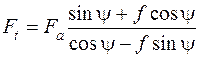. (5.4)

Отримали силу, яку треба прикласти до вантажу, щоб він рухався угору.

Відомо, що , (5.5)
де j – кут тертя. Підставляючи (5.5) у (5.4), отримаємо:

. (5.6)

Добуток рушійної сили 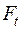на середній радіус дає момент у гвинтовій парі:

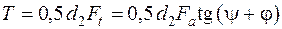. (5.7)

При відгвинчуванні гайки, тобто при опусканні вантажу по похилій площині вниз, аналогічно можна отримати:

. (5.8)

Із виразу (5.8) виходить, що:

1) якщо 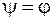, то , тобто вантаж буде знаходитись у стані спокою;

2) якщо 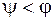, то , тобто вантаж буде знаходитись у стані спокою на площині і для його руху необхідно прикласти якесь додаткове навантаження;

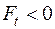3) якщо , то , тобто вантаж буде рухатись вниз під дією своєї ваги без дії додаткової сили.

Таким чином, умовою спокою вантажу на похилій площині, тобто умовою самогальмування різьби буде:

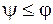. (5.9)

Коефіцієнт корисної дії визначається відношенням роботи сил корисного опору 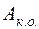до роботи рушійних сил .

При підйомі вантажу по похилій площині рушійною силою 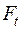на висоту, рівну кроку різьби р, робота рушійних сил 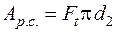, а робота сил корис­ного опору .

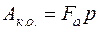Коефіцієнт корисної дії гвинтової пари з прямокутною різьбою при нагвинчуванні гайки:

. (5.10)

Підставляючи у рівняння (5.10) р із (5.1) і 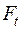із (5.6), отримаємо

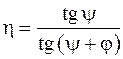. (5.11)

Визначимо сили тертя й установимо співвідношення між силами тертя в прямокутній і трикутній різьбах.

Рис. 5.6. Розрахункова схема до визначення співвідношень сил, що діють у прямокутній (а) і трикутній (б) різьбах

Сила тертя для прямокутної різьби (рис. 5.6, а) 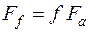, де f – коефіцієнт тертя.

Сила тертя для трикутної різьби (рис. 5.6, б) , де a – кут профілю різьби; – приведений коефіцієнт тертя;

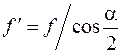. (5.12)

Отримане співвідношення спра­ведливе і для трапецеїдальної різьби.

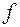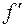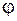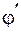Співвідношенню коефіцієнтів тертя і відповідає співвідношення між кутами тертя і , де 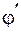– приведений кут тертя:

.

Співвідношення між силами в прямокутній і трикутній різьбах аналогічні. Тому за аналогією з формулами (5.6), (5.7) і (5.9) випливає, що для трикутної (трапецеїдальної, упорної) різьби

окружна сила

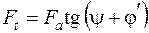; (5.13)

крутний момент у різьбі

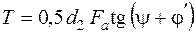; (5.14)

умова самогальмування

; (5.15)

коефіцієнт корисної дії

. (5.16)

Рис. 5.7. Розрахункова схема до визначення моменту сил тертя на торці головки гайки (гвинта)

Визначимо момент тертя на торці гайки або головки гвинта (рис. 5.7) при їхньому загвинчуванні. Питомий тиск на опорній поверхні

,

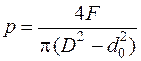де 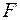– сила притиснення гайки або головки гвинта.

Момент тертя на торці гайки або головки гвинта , звідки

. (5.17)

Для спрощення розрахунків приймають, що рівнодійна сила тертя 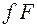на опорній поверхні гайки або головки гвинта діє по дотичній до кола середнього діаметра 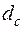опорної поверхні. Тоді момент

, (5.18)
де .

Таким чином, момент загвинчування гайки чи гвинта

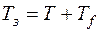. (5.19)