Задание
1. Установите подвижные грузы M на минимальном расстоянии от оси вращения и, сделав 2–3 выстрела, определите приближенно угол отклонения θ1 маятника при попадании в него пули.
2. Оцените по формуле (7) Δθсист. Для этого отклоните маятник из положения равновесия на угол θ1, отпустите без толчка и измерьте
амплитуду θ2 второго отклонения маятника в ту же сторону. Измерения повторите три раза и найдете среднее арифметическое значение θ2. Результате измерений занесите в табл. 1.
Таблица 1
| θ1 | θ2,1 | θ2,2 | θ2,3 | 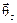
| Δθсист | Δθо |
Сравните найденное значение Δθсист с погрешностью Δθо измерений угла по шкале устройства (Δθо равно половине цены деления шкалы).
3. Определите То. Для этого измерьте периоды колебаний маятника Т1 и Т2 при двух различных положениях R1 ≈ Rmin и R2 ≈ Rmax пар подвижных грузов M. Результаты измерений занесите в табл. 2
Таблица 2
| R1 | 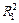
| ΔR1 | R2 | 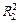
| ΔR2 | T1 | 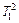
| T2 | 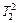
| M | Io | ΔIo |
4.Установив на расстоянии R ≈ Rmin грузы M, измерьте отклонение маятника θ = θmax и прицельное расстояние l в серии из четырех выстрелов. Результаты измерений занесите в табл. 3.
Таблица 3
| l1 | l2 | L3 | l4 | 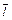
| Δl | θ1 | θ2 | θ3 | θ4 | 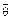
| Δθ | 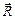
| 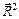
| 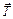
| Δ T | 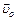
| Δυо |
Пользуясь соотношением (5), определите скорость пули.
Можно ли утверждать, что скорость пуль в серии выстрелов одинакова в пределах точности измерений или имеется разброс в скорости пуль от выстрела к выстрелу?
5. Измерьте приближенно глубину Sо, на которой пуля застревает при попадании в маятник. Оцените по формуле (8) время соударения τ пули с маятником, полагая в (8) n = 10. Убедитесь в том, что неравенство (6) в условиях опыта действительно выполняется.
Задачи
1. Два тела (m1=3 кг, m2=2 кг), двигавшиеся навстречу друг другу (υ1=2 м/c, υ2=3 м/с) после неупругого удара:
Ответы: 1) будут двигаться вправо со скоростью 2 м/с; 2)будут двигаться вправо со скоростью 1 м/с; 3) остановятся; 4) будут двигаться влево со скоростью 1 м/с; 5) будут двигаться со скоростью 2 м/с.
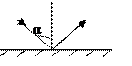
2. Чему равен модуль изменения импульса тела массой m при абсолютно упругом ударе о
некоторую плоскую поверхность, как показано на рисунке?
Ответы: 1) mυ cosα; 2) 2 mυ cosα; 3) mυ sinα; 4) 2 mυ sinα; 5) mυ(cosα–sinα)
3. Тело массой 0,2 кг падает с высоты 1 м с ускорением 8м/с. Найти изменение импульса.
Ответы:1) 10,3 кг.м/с; 2) 0,6 кг.м/с; 3) 0,8 кг.м/с; 4) 3,2 кг.м/с; 5) 1,2 кг.м/с.
4. Два шара массами 6 кг и 4 кг движутся вдоль одной прямой со скоростями 8 м/с и 3 м/с. С какой скоростью они будут двигаться после абсолютно неупругого удара, если первый шар догоняет второй?
Ответы:1) 12,7 м/с; 2) 10 м/с; 3) 5,7 м/с; 4) 6 м/с; 5) 8,0 м/с.
5. Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Найти скорость вагона, если он двигался со скоростью 10 м/с навстречу снаряду
Ответы:1) 7,62 м/с; 2) 12,8 м/с; 3) 9,35 м/с; 4) 4,54 м/с; 5) 5,76 м/с.
6. Молекула массой 5.10–26 кг, летящая со скоростью 500 м/с, упруго ударяется о стенку под углом 300 к перпендикуляру. Найти импульс силы, полученный стенкой при ударе:
Ответы:1) 7,26.10–23 Н.с; 2) 9.10–22 Н.с; 3) 2,34.10–22 Н.с; 4) 6,8.10–22 Н.с; 5) 4,32.10–23 Н.с.
Дата добавления: 2015-10-05; просмотров: 669;
