Измерения. Соотношение (1), использовавшееся при выводе выражения (5), было получено для идеализированной модели
Соотношение (1), использовавшееся при выводе выражения (5), было получено для идеализированной модели, а именно, предполагалось, что выполнены следующие условия:
1) колебания маятника являются незатухающими;
2) время τ соударения пули с маятником мало по с равнению с периодом колебаний:
τ << T (6)
(баллистический режим).
Поэтому прежде всего необходимо выяснить, обеспечивается ли выполнение этих условий для имеющейся лабораторной установки.
Сначала обсудим первое из них. Отклонив маятник из положения равновесия, легко убедиться, что амплитуда его колебаний довольно быстро уменьшается. Следовательно, модель незатухающих колебаний не является точной и применение полученной в рамках этой модели формулы (5) может привести к систематической погрешности в определении скорости пули.
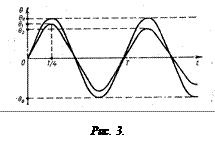
Оценим эту погрешность, для чего сравним графики зависимости амплитуды незатухающих и затухающих колебаний маятника от времени. Будем считать, что в обоих случаях маятник выведен из положения равновесия в момент времени t = 0 с одинаковой начальной скоростью (рис. 3).
Как видно из рисунка, пренебрежение затуханием приводит к заниженному значению скорости пули. Действительно, в формулу (5) подставляется измеренная величина θ1 = θmax, а она меньше, чем соответствующая той же начальной скорости амплитуда незатухающих колебаний θ0. Следовательно, при определении θmax возникает систематическая погрешность, равная
Δθсист = θ1 – θ0.
Для оценки заметим, что она накапливается за четверть периода колебаний, т.е. за время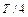 
. Уменьшение амплитуды колебаний за полный период Т можно измерить непосредственно:
Δθ = θ2 – θ1,
где θ1 и θ2 – соответственно углы первого и второго максимального отклонения маятника после попадания в него пули. Считая зависимость амплитуды затухающих колебаний от времени приблизительно линейной (для этого нужно, чтобы затухание за период было мало), находим
.
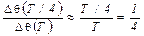Следовательно,
,
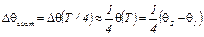т.е.
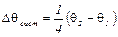. (7)
Если θ1 и θ2 совпадают в пределах точности, с которой измеряется угол отклонения θ маятника, то Δθсист, очевидно, можно пренебречь и модель незатухающих колебаний справедлива.
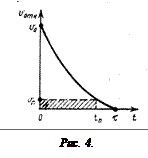
Попробуем теперь оценить τ (τ – время соударения пули с маятником). Построим качественно график зависимости скорости пули от времени относительно маятника (рис. 4.)
Непосредственно перед соударением маятник покоится, а скорость пули равна υо: значит, их начальная относительная скорость υотн (0) = υо. В конце удара, т.е. при t = τ, по определению, υотн (τ) = 0.
Естественно считать, что в течение удара скорость υотн постепенно (монотонно) убывает от υо до нуля. Без проведения специальных измерений ничего более определённого сказать о зависимости υотн от t нельзя: для этого необходимо заранее знать закон взаимодействия между соударяющимися телами. Нам же надо лишь приближенно оценить τ.
Пусть tn – момент, когда относительная скорость пули уменьшается по сравнению с начальной в n раз:
.
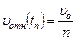Из рис.3 видно, что полное перемещение пули в материале маятника
,
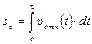равное полной площади под кривой υотн (t), заведомо превышает площадь заштрихованного прямоугольника:
.
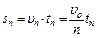При достаточно больших значениях n, например при n > 10, можно считать, что tn мало отличается от времени соударения τ, и положить τ ≈ tn. Тогда получаем неравенство
,
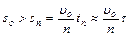которое позволяет получить оценку τ:
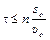. (8)
Величины, стоящие в правой части неравенства (8), определяются на опыте. В лабораторной установке глубина проникновения пули в маятник sо ≤ 0,5 см, а скорость пули υо ≥ 1 м ∕с.
Следовательно,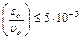 
с и при n = 10 получаем для τ оценку сверху: τ≤0,05 с.
Так как период колебаний маятника Т ≈ 1 с, то можно считать, что равенство (6) в этих условиях выполняется.
Примечание.Выбор величины n = 10 может показаться произвольным. Однако при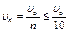 
практически можно считать, что удар действительно «закончился», так как к этому моменту кинетическая энергия пули
,
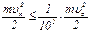т.е. составляет всего лишь примерно 1 % её первоначальной кинетической энергии.
Выясним теперь, как определить в рабочей формуле неизвестную величину Iо. Для этого запишем период колебания маятника в виде
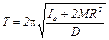.(9)
Таким образом, Т зависит от расстояния R центров подвижных грузов M от оси вращения.
Установив грузы M на некотором расстоянии R1 от оси вращения, можно определить период колебаний T1 маятника. Сместим грузы M в другое положение R2 и снова измерим период колебаний T2 маятника. Так как [см. (9)]
,
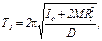
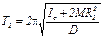то, исключая из этих равенств D, находим
.
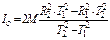Для уменьшения погрешности, с которой определяется величина Iо, расстояния R1 и R2 следует взять заметно отличающимися друг от друга. Лучше всего взять R1 возможно ближе к оси вращения, а R2 – на максимальном расстоянии от неё.
После того как найдено Iо, скорость пули может быть определена из формулы (5) по известным значениям массы m пули, масс M грузов и измеряемым на опыте значениям периода колебаний T, прицельного расстояния l, расстояния R и угла отклонения θmax маятника.
Для повышения точности измерений рекомендуется устанавливать грузы M на небольшом расстоянии R от оси маятника, чтобы угол отклонения θmax маятника был как можно больше.
Дата добавления: 2015-10-05; просмотров: 473;