Теория метода. Для расчета момента инерции тела относительно произвольной оси необходимо знать момент инерции подвеса крутильного маятника и модуль кручения

Для расчета момента инерции тела относительно произвольной оси необходимо знать момент инерции подвеса крутильного маятника и модуль кручения. Для определения этих величин измеряют период крутильных колебаний для двух случаев:

1) без дополнительного груза T₁;

2) с дополнительным грузом Т₂ (цилиндром), момент инерции которого легко рассчитать теоретически (например цилиндра):

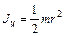, (6)

где m–масса цилиндра, r–радиус цилиндра.

Запишем период крутильных колебаний для этих случаев:

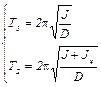(7)

где J_ц – момент инерции цилиндра, D – модуль кручения, J – момент инерции подвеса крутильного маятника.

Возведем оба уравнения в квадрат и разделим друг на друга:

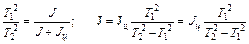. (8)

Подставим (8) в первое уравнение системы (7) и разрешим относительно D

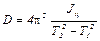. (9)

Рассчитав модуль кручения и момент инерции подвеса можно преобразить вторую формулу в системе (7), в которой вместо J_ц уже стоит искомый момент инерции тела J_x.

:

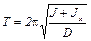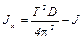. (10)