Основні поняття систем лінійних рівнянь

Лекція №1. Системи лінійних рівнянь, визначники

ПЛАН

Основні поняття систем лінійних рівнянь

2. Визначники другого і третього порядків, їх властивості

3. Мінори та алгебраїчні доповнення

4. Обчислення визначників

Основні поняття систем лінійних рівнянь

Предметом розгляду лінійної алгебри є насамперед теорія систем лінійних рівнянь, які в загальному вигляді можна подати так:

(1.1)

Означення 1. Система (1.1) називається системою m лінійних рівнянь з n невідомими (змінними), де x₁, x₂, ..., x_n — невідомі; a_ij 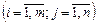— коефіцієнти системи рівнянь; b_i — вільні члени, або праві частини системи рівнянь. Якщо всі b_i = 0 , то система лінійних рівнянь називається однорідною.

Означення 2. Розв’язком системи рівнянь (1.1) є множина таких чисел k₁, k₂, ..., k_n, у результаті підставляння яких замість відповідних невідомих x₁, x_2, ..., x_n у кожне з рівнянь системи (1.1) останні перетворюються на правильні числові рівності.

Означення 3. Системалінійних алгебраїчних рівнянь називається несумісною, якщо дана система рівнянь не має жодного розв’язку.

Означення 4. Системалінійних алгебраїчних рівнянь називається сумісною, якщо вона має хоча б один розв’язок.

Означення 5. Системалінійних алгебраїчних рівнянь називається визначеною, якщодана система сумісна та має єдиний розв’язок.

Означення 6. Системалінійних алгебраїчних рівнянь називається невизначеною, якщо дана система сумісна та має більш як один розв’язків.

2. Визначники другого і третього порядків, їх властивості

Розглянемо спочатку системи рівнянь, в яких кількість невідомих і кількість рівнянь рівні між собою, тобто m=n. Нехай, наприклад, n=m=2, тоді маємо систему двох лінійних рівнянь з двома невідомими:

Означення 7. Визначником другого порядку називається вираз

.

Визначник (детермінант) позначається , або det