Тонкие линзы. Изображение предметов с помощью линз
Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии.Геометрическая оптика, оставаясь приближенным методом построения изображений в оптических системах, позволяет разобрать основные явления, связанные с прохождением через них света, и является, поэтому основой теории оптических приборов.
Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями одна из них обычно сферическая, иногда цилиндрическая, а вторая — сферическая или плоская, преломляющими световые лучи, способные формировать оптические изображения предметов.
 Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п.
Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п.
По внешней форме (рис.25.3) линзы делятся на: 1)двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые.
По оптическим свойствам линзы делятся на собирающие и рассеивающие. Рис.25.3.
Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу.
Прямая, проходящая через центры кривизны поверхностей линзы называется главной оптической осью.
Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь.
Формула тонкой линзы — соотношения, связывающего радиусы кривизны R1 и R2 поверхностей линзы с расстояниями а и b от линзы до предмета и его изображения
(n21 – 1)( 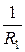 +
+ 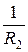 ) =
) = 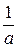 +
+  . (25.13)
. (25.13)
Формула тонкой линзыгде n21 =n2/n1относительный показатель преломления (n2и n1–соответственно абсолютные показатели преломления линзы и окружающей среды).
 Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой — отрицательным.
Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой — отрицательным.
Если а=∞, т. е. лучи падают на линзу параллельным пучком (рис.25.4, а), то
( n21 – 1) ( 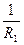 +
+ 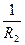 ) =
) = 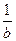 . (25.14)
. (25.14)
Соответствующее этому случаю расстояние b=ОF=f называется фокусным расстоянием линзы, определяемым по формуле Рис. 25.4.
f =  . (25.15)
. (25.15)
Оно зависит от относительного показателя преломления и радиусов кривизны.
Если b = ∞, т.е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком (рис.25.4.б), то а = ОF = f.
Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны.
Точки F, лежащее по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус — это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.
Плоскости, проходящие через фокусы линзы перпендикулярно главной оптической оси, называются фокальными плоскостями.
Величина
Ф=  = ( n21 – 1)(
= ( n21 – 1)( 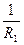 +
+ 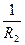 )
)
называется оптической силой линзы. Ее единица — диоптрия (дптр).Диоптрия  оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м.
оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м.
Линзы с положительной оптической силой являются собирающими, с отрицательной — рассеивающими.
Построение изображения предмета в линзах осуществляется с помощью следующих лучей:
1) луча, проходящего через оптический центр линзы
и не изменяющего своего направления; Рис.25.5.
2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;
3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси.
Для примера приведены построения изображений в собирающей (рис.25.5) линзе: действительное (рис. 25.5.а) и мнимое (рис. 25.5.б) изображения.
Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным — мнимое изображение (оно прямое).
Комбинации собирающих и рассеивающих линз применяются в оптических приборах, используемых для решения различных научных и технических задач.
Дата добавления: 2015-10-05; просмотров: 1826;
