И потенциалом
Работа сил поля над зарядом 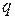 на отрезке пути
на отрезке пути 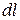 может быть представлена, с одной стороны, как
может быть представлена, с одной стороны, как 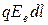 , с другой же стороны как убыли потенциальной энергии заряда, т.е. как
, с другой же стороны как убыли потенциальной энергии заряда, т.е. как 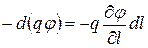 . Приравнивая эти выражения, получим
. Приравнивая эти выражения, получим
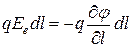 ,
,
откуда находим, что
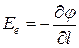 ,
,
где через 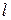 обозначено произвольно выбранное направление в пространстве. В частности,
обозначено произвольно выбранное направление в пространстве. В частности,
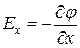 ,
, 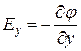 ,
, 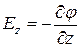 ,
,
откуда 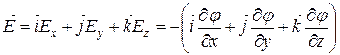 .
.
Выражение, стоящее в скобках, называется градиентом скаляра j (обозначается 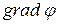 ). Используя обозначения градиента, можно написать:
). Используя обозначения градиента, можно написать:
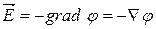 , (Ñ - набла).
, (Ñ - набла).
Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком. Направление градиента совпадает с направлением 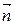 , в котором при смещении из дано точки функция j, возрастая по величине, изменяется с наибольшей скоростью.
, в котором при смещении из дано точки функция j, возрастая по величине, изменяется с наибольшей скоростью.
Величина производной 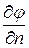 по этому направлению дает модуль градиента. Частные производные
по этому направлению дает модуль градиента. Частные производные 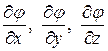 представляют собой проекции градиента на координатные оси
представляют собой проекции градиента на координатные оси 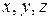 . Проекция градиента на ^ к нему направление t, очевидно, равна нулю:
. Проекция градиента на ^ к нему направление t, очевидно, равна нулю: 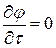 .
.
Поясним соотношения между напряженностью поля и потенциалом на примере поля точечного заряда. Потенциал этого поля выражается функцией 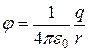 .
.
 Рассмотрим точку поля 1, положение которой определяется радиусом-вектором
Рассмотрим точку поля 1, положение которой определяется радиусом-вектором 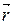 . При смещении из этой точки в разных направлениях на одинаковой величине малый отрезок
. При смещении из этой точки в разных направлениях на одинаковой величине малый отрезок 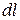 наибольшее
наибольшее
Рис. 13.8. положительное приращение j получается для
направления от точки 1 к заряду 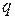 , если он положителен, и от заряда
, если он положителен, и от заряда 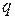 к точке 1, если отрицателен. Следовательно, направление градиента
к точке 1, если отрицателен. Следовательно, направление градиента 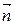 может быть представлено в виде
может быть представлено в виде
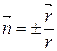 ,
,
где (-) соответствует положительному заряду, а (+) – отрицательному. Проекция 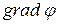 на направление
на направление 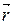 равна
равна
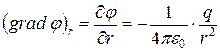
или 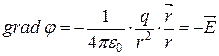 .
.
Дата добавления: 2015-10-05; просмотров: 628;
