Потенциал. Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.
Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.
Работу можно представить в виде разности значений потенциальной энергии, которой заряд q¢ обладал в точках 1 и 2 поля заряда q:
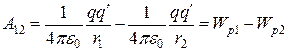 .
.
Отсюда для потенциальной энергии заряда q¢ в поле заряда q получаем
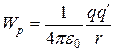 . (13.14)
. (13.14)
Разные пробные заряды 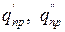 … будут обладать энергией
… будут обладать энергией 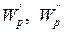 … Однако отношение
… Однако отношение 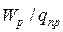 будет для всех зарядов одно и то же. Величина
будет для всех зарядов одно и то же. Величина
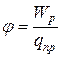 (13.15)
(13.15)
называется потенциалом поля в данной точке и используется, наряду с напряженностью поля 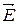 , для описания электрических полей.
, для описания электрических полей.
Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Подставляя в (13.15), значение потенциальной энергии (13.14), получим для потенциала поля точечного заряда следующее выражение:
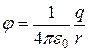 . (13.16)
. (13.16)
Рассмотрим поле, создаваемой системой точечных зарядов  Расстояние от каждого из зарядов до данной точки поля обозначим
Расстояние от каждого из зарядов до данной точки поля обозначим 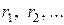 Работа, совершаемая силами этого поля над зарядом
Работа, совершаемая силами этого поля над зарядом 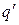 , при переносе из точки 1 в 2, будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
, при переносе из точки 1 в 2, будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
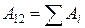 .
.
Каждая из работ 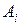 равна
равна
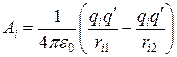 ,
,
где 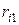 - расстояние от заряда
- расстояние от заряда 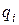 до начального положения заряда
до начального положения заряда 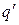 ,
, 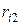 - расстояние от заряда
- расстояние от заряда 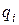 до конечного положения заряда
до конечного положения заряда 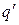 . Следовательно
. Следовательно
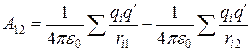 .
.
Сопоставляя это выражение с соотношением
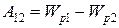 ,
,
получаем для потенциальной энергии заряда 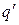 в поле системы зарядов выражение
в поле системы зарядов выражение
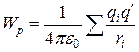 ,
,
отсюда
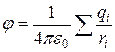 . (13.17)
. (13.17)
Таким образом, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Так как потенциалы складываются алгебраически, то их вычисление проще чем вычисление напряженностей электрического поля.
Из (13.15) следует, что заряд 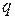 , находящийся в точке поля с потенциалом j, обладает потенциальной энергией
, находящийся в точке поля с потенциалом j, обладает потенциальной энергией
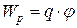 .
.
Следовательно, работа сил поля над зарядом 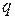 может быть выражена через разность потенциалов:
может быть выражена через разность потенциалов:
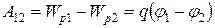 .
.
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках. Если заряд 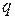 из точки с потенциалом j удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
из точки с потенциалом j удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
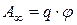 .
.
Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Такую же по величине работу необходимо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
За единицу потенциала в СИ принимается потенциал в такой точке, для перемещения в которую из бесконечности заряда, равного 1 кулону, нужно совершить работу в 1 джоуль:
[j] = В
1В = 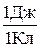 .
.
Дата добавления: 2015-10-05; просмотров: 749;
