Система отсчета. Траектория, длина пути, вектор перемещения

КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ

­

Система отсчета. Траектория, длина пути, вектор перемещения

Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка - тело, обладающее массой, размерами которого в данной задаче мож­но пренебречь. Понятие материальной точки - абстрактное, но его введение облег­чает решение практических задач. Напри­мер, изучая движение планет по орбитам вокруг Солнца, можно принять их за мате­риальные точки.

Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматри­вается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы матери­альных точек. В механике сначала изуча­ют движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Под воздействием тел друг на друга тела могут деформироваться, т. е. изме­нять свою форму и размеры. Поэтому в механике вводится еще одна модель - абсолютно твердое тело. Абсолютно твер­дым телом называется тело, которое ни при каких условиях не может деформиро­ваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается по­стоянным.

Любое движение твердого тела можно представить как комбинацию поступатель­ного и вращательного движений. Поступа­тельное движение - это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллель­ной своему первоначальному положению. Вращательное движение - это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Движение тел происходит в простран­стве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. В системе СИ время измеряется в секундах [t] = c.

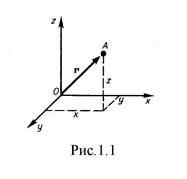
Положение материальной точки опре­деляется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связы­вается система отсчета- совокупность системы координат и часов, связанных с телом отсчета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент вре­мени по отношению к этой системе ха­рактеризуется тремя координатами х, у и z или радиусом-вектором 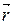, проведен­ным из начала системы координат в дан­ную точку (рис. 1.1).

При движении материальной точки ее координаты с течением времени изменяют­ся. В общем случае ее движение определя­ется скалярными уравнениями

x = x(t),

y = y(t),(1.1)

z = z(t),

эквивалентными векторному уравнению

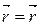(t). (1.2)

Уравнения (1.1) (соответственно (1.2)) называются кинематическими уравнения­ми движения материальной точки.

Число независимых координат, полно­стью определяющих положение точки в пространстве, называется числом степе­ней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z); если она движется по некоторой поверхно­сти, то - двумя степенями свободы, ес­ли вдоль некоторой линии, то - одной степенью свободы.

Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки - ли­ния, описываемая этой точкой в простран­стве. В зависимости от формы траектории движение может быть прямолиней 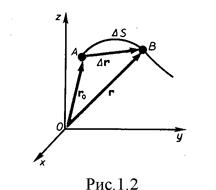ным или криволинейным.

Рассмотрим движение материальной точки вдоль произвольной траектории (рис.1.2). Отсчет времени начнем с момен­та, когда точка находилась в положении А. Длина участка траектории АВ, прой­денного материальной точкой с момента начала отсчета времени, называется дли­ной пути Δs и является скалярной функцией времени в Δs = Δs(t). Размерность пути в СИ- метр (м). Вектор 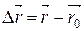, проведенный из начального положе­ния движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматривае­мый промежуток времени), называется пе­ремещением.

При прямолинейном движении вектор перемещения совпадает с соответствую­щим участком траектории и модуль пе­ремещения 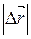равен пройденному пу­ти Δs.