Логических функций одной переменной всего четыре. Они приведены в таблице 3.2.
Таблица 3.2 – Логические функции одной переменной
| x | j0 | j1 | j2 | j3 |
Функции j0 и j3 – константы 0 и 1 соответственно; их значения не зависят от значения переменной, и , следовательно, переменная x для них несущественна. Функция j1 повторяет x. Функция j2 называется "отрицанием" или функцией "НЕ" и обозначается 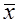 или
или 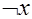 . Ее значение противоположно значению x.
. Ее значение противоположно значению x.
Логических функций двух переменных – 16. Они приведены в таблице 3.3.
Таблица 3.3 – Логические функции двух переменных
| x1 x2 | j0 | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 | j13 | j14 | j15 | |
| 0 0 | |||||||||||||||||
| 0 1 | |||||||||||||||||
| 1 0 | |||||||||||||||||
| 1 1 |
Функции j0 и j15 константы 0 и 1, т.е. функции с двумя несущественными переменными. Отметим, что эти функции отличаются от приведенных в таблице 3.2. Там они унарные, а здесь бинарные операции на В.
Функция j1 называется конъюнкцией х1 и х2; ее обозначают: 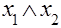 или
или 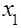 &
& 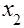 . Во всех случаях знак конъюнкции аналогично знаку умножения часто опускают и пишут х1 х2 . Она равна 1, только если х1 и х2 равны 1, поэтому ее часто называют функцией И. Еще одно ее название – "логическое умножение", поскольку ее таблица действительно совпадает с таблицей обычного умножения для чисел 0 и 1.
. Во всех случаях знак конъюнкции аналогично знаку умножения часто опускают и пишут х1 х2 . Она равна 1, только если х1 и х2 равны 1, поэтому ее часто называют функцией И. Еще одно ее название – "логическое умножение", поскольку ее таблица действительно совпадает с таблицей обычного умножения для чисел 0 и 1.
Функция j7 называется дизъюнкцией х1 и х2; ее обозначают: 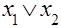 или
или 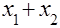 . Она равна 1, если х1 или х2 равен 1 ("или" здесь понимается в неразделительном смысле – хотя бы одно из двух). Поэтому ее часто называют функцией ИЛИ.
. Она равна 1, если х1 или х2 равен 1 ("или" здесь понимается в неразделительном смысле – хотя бы одно из двух). Поэтому ее часто называют функцией ИЛИ.
Функция j6 – это сложение по модулю 2. Ее обозначение х1Åх2. Она равна 1, когда значения ее аргументов различны, и равна 0, когда они равны.
Другие функции имеют название: j13 – импликация: х1®х2; j8 – стрелка Пирса: х1¯х2; j14 – штрих Шеффера: х1 ½ х2.
Дата добавления: 2015-10-05; просмотров: 1200;
