ОПРЕДЕЛЕНИЕ ИСТИНОЙ ДЛИНЫ ОТРЕЗКА И УГЛА ПАДЕНИЯ ПРЯМОЙ.

СУЩНОСТЬ МЕТОДА. ПРОЕКЦИИ ТОЧЕК НА ПЛАНЕ.

В прямоугольных проекциях изображенный предмет проецируют на две и более плоскостей проекций. Но если вертикальные размеры изображаемого предмета существенно невелики по сравнению с горизонтальными (длиной и шириной), то построение фронтальной проекции затруднено, а практическое ее использование неудобно. В таком случае пользуются особым методом построения изображений, называемым методом проекций с числовыми отметками. Наибольшее применение этот метод нашел в решении задач при горном и геологоразведочном производстве.

Сущность метода проекций с числовыми отметками заключается в следующем. Изображаемый предмет прямоугольно проецируют только на одну горизонтально расположенную плоскость проекций П₀, называемую плоскостью нулевого уровня. На чертеже в этом случае отображаются только два его измерения: длина и ширина. Третье измерение – высота изображаемого предмета – выражается числами, определяющими расстояние от точек предмета до плоскости проекций. Условимся в дальнейшем эти числа называть числовыми отметками. Плоскость проекций П₀, относительно которой ориентируют точки пространства, называют основной или плоскостью нулевого уровня. В решении географических, геодезических и геологических задач за такую плоскость принимают уровень воды моря и океана. В России все абсолютные высоты отсчитываются от нуля Кронштадтского футштока. Изображение в проекциях с числовыми отметками называется планом.

Для полного определения пространственного расположения изображенных на чертеже точек необходимо наличие масштаба (масштаб всегда указывается на чертеже) и указания линейной единицы, в которой выражены числовые отметки.

На рис.2.1, а изображены точки A, B и C. Основания перпендикуляров, опущенных из этих точек на плоскость П₀, являются их проекциями на эту плоскость. Проекция каждой точки определяет две координаты точки в пространстве: по оси xи по оси y. Третья координата по оси z – высота точки – определяется числом. Точка A находится над П₀ и отстоит от нее на расстояние 3 ед. длины. Точка B находится под плоскостью П₀ на расстоянии 2 ед. длины. Эти числа указаны около проекций точек A и B. Числовые отметки точек, расположенных ниже плоскости П₀, имеют отрицательный знак (В_-2). Точка C, принадлежащая плоскости нулевого уровня, имеет нулевую отметку (C₀). На рис.2.1, б дан план, на котором показаны проекции точек A, B и C с их числовыми отметками.

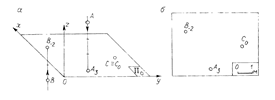
Рис. 2.1

В решении практических задач геодезии, а также маркшейдерии возможен случай перехода от одной плоскости проекций к другой: новую плоскость проекций располагают параллельно П₀, но выше или ниже ее (рис 2.2). Расположение точек в пространстве остается неизменным, поэтому положение их проекций не изменяется, изменяются только отметки точек. Если новую плоскость расположить выше первоначальной, то положительные отметки всех точек уменьшатся на n ед. (на рис 2.2 на 2 ед.), а отрицательные - увеличатся на n ед. (на рис 2.2 на 2 ед.). Если плоскость проекций расположить ниже, то отрицательные отметки всех точек уменьшатся на n ед., а положительные - увеличатся на n ед. (на рис 2.2 на 3 ед.). Числовая отметка, выражающая удаление точки от плоскости проекций, называется абсолютной, от произвольно взятой плоскости проекций – условной.

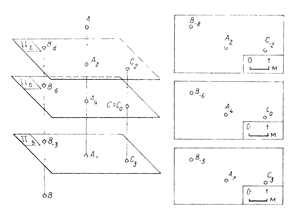
Рис. 2.2

КЛАССИФИКАЦИЯ ПРЯМЫХ И СПОСОБЫ ЗАДАНИЯ ПРЯМОЙ НА ПЛАНЕ.

В основу классификации прямых берут их расположение относительно плоскости проекций. Получают три вида прямых: наклонные, горизонтальные и вертикальные.

Наклонные прямые. Наклонная прямая m (рис. 2.3, а) не параллельна и не перпендикулярна к плоскости проекций и может быть определена: 1) двумя точками – m(А₁В₄), рис 2.3, б; 2) точкой B, направлением наклона (на плане показана стрелкой) и величиной угла наклона к плоскости проекций П₀ – m(В₄Ð40⁰) (рис. 2.3., в). Определитель прямой условимся указывать в скобках.

Под определителем прямой будем понимать совокупность условий, необходимых и достаточных для ее одинакового задания. На рис. 2.3, б прямая m задана на плане двумя указанными способами.

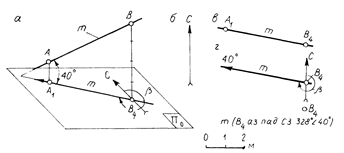
Рис. 2.3

У наклонной прямой различают два направления: направление падения и противоположное ему направление восстания. Каждое из направлений с северным направлением меридиана составляет на плане угол, который носит название азимута. Угол b (азимут) отсчитывают по ходу часовой стрелки (рис. 2.3, в).

В горно-геологической практике, помимо перечисленных выше двух способов, используется задание прямой ее элементами залегания: точкой, азимутом падения и углом наклона прямой к плоскости проекций, который носит название угла падения прямой. Под азимутом падения понимают правый угол, составленный на плане северным направлением меридиана и направлением падения прямой. Определитель прямой записывается в следующем порядке (рис. 2.3): m (В₄ аз. пад. СЗ 328⁰ Ð40⁰). Кроме угловой величины азимута (для большей ясности) указывают и азимутальную четверть (СВ, ЮВ, ЮЗ, СЗ), в которой этот угол находится. На плане проекция отрезка наклонной прямой m меньше его наклонной длины: ½А₁В₄½<½АВ½.

Горизонтальная прямая. Прямая h (C₂D₂) параллельна плоскости проекций (рис. 2.4, а). Такую прямую называют горизонтальной. Горизонтальная прямая проходит через точки, расположенные на одной и той же высоте. Поэтому на чертеже (рис. 2.4, а) такую прямую можно задать проекцией с указанием высоты, на которой она проходит, - h₂.

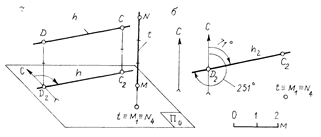
Рис. 2.4

У горизонтальной прямой различают два направления, которые носят название направлений простирания. На плане с северным направлением меридиан они составляют углы, которые называют азимутами простирания. Под азимутом простирания понимают правый угол, составленный на плане северным направлением меридиана и одним из направлений простирания прямой. Второе направление простирания образует азимут, величина которого больше первого на 180⁰. Определитель горизонтальной прямой записывается в следующем порядке: h(D₂ аз. пр. 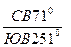). Отрезок горизонтальной прямой проецируется без искажения: ½C₂D₂½=½CD½, так как a=0⁰, cos0⁰=1.

Вертикальная прямая. Прямая t (M₁N₄), перпендикулярная к основной плоскости проекций, показана на том же рис. 2.4, а. Такую прямую называют вертикальной. Проекция вертикальной прямой вырождается на плане в точку (рис. 2.4, б). Проекции точек M и N, принадлежащих вертикальной прямой, совпадают: M₁ºN₄. Точки, проекции которых на плане совпадают, называются конкурирующими.

Истинную длину отрезка вертикальной прямой можно определить аналитически как разность числовых отметок его концов: ½NM½=4-1=3 м.

ОПРЕДЕЛЕНИЕ ИСТИНОЙ ДЛИНЫ ОТРЕЗКА И УГЛА ПАДЕНИЯ ПРЯМОЙ.

Истинную длину отрезка наклонной прямой n, а также угол ее падения можно определить построением ее профиля (рис. 2.5). Через прямую n проводят вспомогательную вертикальную плоскость T, которую в дальнейшем условимся называть плоскостью профиля прямой (рис. 2.5, а). Плоскость профиля совмещают с плоскостью чертежа наложением ее на свободное от построений место (рис. 2.5,б). Построенная проекция отрезка (профиль отрезка) равна его истинной длине. Угол a, составленный профилем отрезка и линией горизонта, является углом падения прямой n.

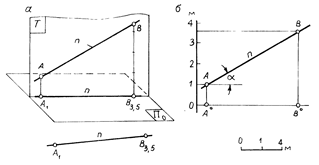
Рис. 2.5

Построение профиля прямой n сводится к построению ее вертикальной проекции и проводится в следующем порядке:

1) на свободном месте чертежа наносят линию вертикального масштаба (при решении метрических задач вертикальный масштаб берут равным горизонтальному - рис. 2.5, б);

2) на произвольно выбранном горизонте (в рассматриваемом примере на горизонте 0 метров) отмечают положение горизонтальных проекций заданных точек А и В, соблюдая равенство: ½А⁰В⁰½=½А₁В_3,5½. Точки А⁰ и В⁰ условимся в дальнейшем называть основаниями точек;

3) через основания точек проводят линии вертикальной связи до пересечения их с горизонтами 1 и 3,5 в точках А и В. Точки А и В определяют профиль прямой n. Угол a, составленный профилем прямой n и линией горизонта, определяет наклон прямой к плоскости проекций. Отрезок АВ определяет истинное расстояние между точками А и В.

В практике решения горно-геологических задач построенное изображение носит название профиля разреза, выполненного плоскостью T по направлению прямой n.

На рис. 2.6 дан пример построения профиля прямой d, заданной на плане точкой R, направлением падения и углом падения 30° (рис. 2.6, а). Построение профиля и в этом случае начинают с проведения масштабной вертикальной линии (рис. 2.6, б). На горизонте 4,5 метров отмечают точку R, через которую проводят профиль прямой d, пересекающий линию горизонта под углом 30°.

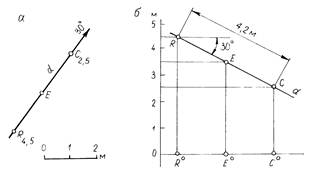
Рис. 2.6

По профилю прямой можно построить на плане проекцию точки С, принадлежащую прямой d и удаленной от точки R на расстояние 4,2 м, а также построить проекцию точки Е с заданной числовой отметкой. Решение задачи в первом случае:

1) на профиле прямой d, отложив от точки R длину 4,2 м, отмечают точку С;

2) определяют основание – С° и высотную отметку точки – 2,6 м;

3) строят проекцию точки C на плане, исходя из равенства:½R⁰C⁰½=½R_4,5C_2,6½.

Во втором случае проекцию точки с отметкой 3,5 м определяют проведением линии соответствующего горизонта до пересечения ее с профилем прямой в точке Е. Построив основание Е⁰, строят проекцию точки Е на плане: ½R⁰E⁰½=½R_4,5E_3,5½.

На рис. 2.7 рассматривается другой метод построения профиля прямой m, заданной на плане точками A и B. Вертикальную плоскость T (плоскость профиля прямой) вращением вокруг линии пересечения ее с плоскостью проекций совмещают с плоскостью чертежа (рис. 2.7, а). На плане построение профиля прямой проводят в следующем порядке: через точки А₁ и В₃ перпендикулярно к проекции прямой mпроводят линии проекционных связей, на которых в масштабе плана откладываются высоты точек A и B. 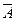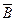Точки ₀ и ₀ определяют профиль прямойm. Профиль отрезка равен его истинной длине ½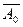 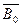½=½AB½ (рис. 2.7, б).

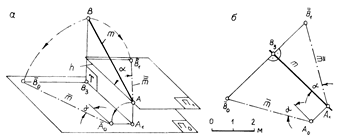
Рис. 2.7

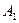
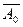
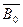
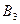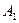
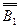
Профиль прямой можно строить, совмещая плоскость T с любой горизонтальной плоскостью. В этом случае плоскость Т вращается вокруг линии пересечения ее с горизонтальной плоскостью П₁. Решение задачи на плане сводится к построению прямоугольной трапеции , либо прямоугольного треугольника 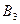, один из катетов которого равен длине проекции отрезка, а второй – разности высот его концов.