ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ.

Различают три случая взаимного расположения двух прямых в пространстве: пересекающиеся, параллельные и скрещивающиеся.

Вопрос о взаимном расположении двух прямых сводится к определению или взаимного расположения их проекций, величин углов падения (заложений) и направлений падения, или взаимного расположения двух точек, принадлежащих данным прямым.

Пересекающиеся прямые. Пересекающиеся прямые имеют общую точку (рис.2.12). Следовательно, на плане проекции таких прямых пересекаются, причем точка пересечения имеет одинаковую отметку. Отметку общей для прямых точки определяют либо интерполированием прямых (рис.2.13), либо построением их профилей (рис.2.14).

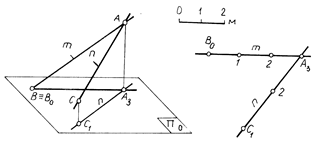
Рис. 2.12

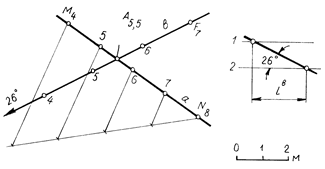
Рис. 2.13

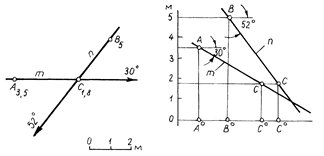
Рис. 2.14

Решая задачу первым способом, построение выполняют в следующем порядке: прямую а интерполируют делением отрезка M₄N₈ на четыре равных части, а прямую в интерполируют с помощью масштаба заложений. Отметка искомой точки А и в одном, и в другом случаях равна 5,5 м, следовательно, точка А является общей для прямых a и b. На рис.2.14 дан другой способ решения задачи. Построив профиль прямых m и n, определяют отметку искомой точки С. В обоих случаях она равна 1,8 м. В целях сокращения количества построений плоскость профиля прямой m совмещают с плоскостью профиля прямой n. При построении профилей прямых расстояние между основаниями точек А и В берут произвольным. В решении графических задач рассмотренный вид построения профилей носит название сводного разреза.

Параллельные прямые. У параллельных прямых m и n углы падения равны (рис.2.15): Ða^m = Ðaⁿ. Равенство углов определяет равенство заложений: l^m = lⁿ. Плоскость профиля прямой m параллельна плоскости профиля прямой n. Следовательно, у параллельных прямых проекции параллельны, заложения равны (углы падения равны), направления падения совпадают: пад.I, т. е. параллельные прямые имеют одинаковые элементы залегания.

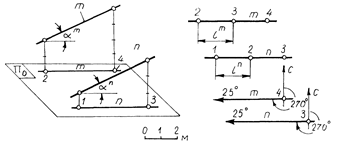
Рис.2.15

Скрещивающиеся прямые. Прямые не пересекающиеся и не параллельные между собой, называются скрещивающимися. Возможны три случая расположения двух скрещивающихся прямых (рис.2.16):

1) проекции прямых m и n пересекаются, но точка пересечения имеет разные числовые отметки, она является проекцией конкурирующих точек А и В, расположенных на одном и том же проецирующем луче (рис.2.16, а);

2) проекции прямых а и b параллельны, но углы падения не равны: Ða^a ¹ Ða^b; заложения также не равны: l^a ¹ l^b (рис.2.16, б);

3) проекции прямых d и t параллельны, заложения равны, но направления падения не совпадают: пад.D(рис.2.16, в).

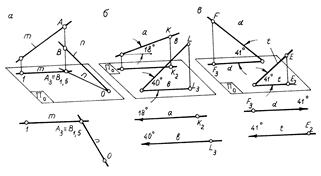
Рис. 2.16

На рис.2.17 взаимное расположение прямых m (А₁₅Ð20°) и n (В_12,5Ð35°) определяется построением профиля сводного разреза, из которого следует, что точка пересечения проекций прямых является проекцией двух различных точек пространства, через которые проходят прямые m и n. Высота точки С не равна высоте точки D. Следовательно, прямые m и n скрещиваются, причем прямая mпроходит над прямой n. Отметим еще один признак, пользуясь которым можно отличать пересекающиеся прямые от скрещивающихся: прямые линии, соединяющие точки с одинаковыми отметками, и в случае пересекающихся прямыхa и b взаимно параллельны (рис.2.18, а), в случае скрещивающихся прямых m и nне параллельны друг другу (рис.2.18, б).

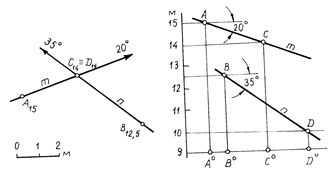
Рис. 2.17

Взаимно перпендикулярные прямые. Линейный угол, образованный двумя пересекающимися прямыми, проецируется без искажения, если обе стороны угла параллельны плоскости проекций. Однако прямой угол проецируется без искажения и том случае, если только одна из его сторон параллельна плоскости проекций. На рис.2.19 изображен прямой угол АВС, стороны которого параллельны плоскости П₀. Он проецируется без искажения, т. е. ÐА₂В₂С₂ = ÐАВС. Отметим на проецирующем луче АА₂ произвольную точку D и соединим ее с точкой В. Полученный угол DBC – тоже прямой, так как отрезок ВС перпендикулярен к плоскости АВВ₂А₂. Точки D и A лежат на одном перпендикуляре к плоскости П₀,

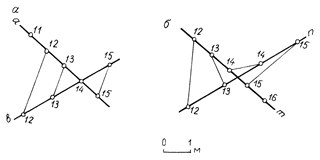
Рис. 2.18

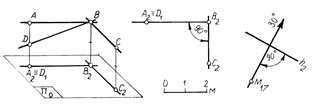
Рис.2.19

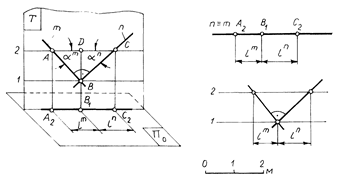
Рис. 2.20

следовательно, проекции углов ABC и DBC совпадут. Отсюда следует, что ÐD₁B₂C₂= ÐA₂B₂C₂ = 90⁰. Это свойство прямого угла дает возможность строить на плане проекции двух взаимно перпендикулярных прямых, одна из которых является горизонталью.

На рис.2.20 дан пример построения на плане проекций двух взаимно перпендикулярных прямых, лежащих в одной вертикальной плоскости T. Проекции прямых m и n на плане совпадают m º n. Сумма углов падения таких перпендикулярных прямых равна 90⁰: Ða^m+ Ðaⁿ = 90⁰. Заложение прямой m обратно пропорционально заложению прямой n: l^m = H/lⁿ. Это следует из прямоугольного треугольника ABC, в котором 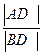= 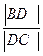; |BD|²=|AD|×|DC| = l^m × lⁿ. Если |BD| принять за единицу, соответствующую выбранной высоте сечения, то уравнение примет вид: 1 = l^m × lⁿ, откуда l^m = 1/lⁿ. Как видно из чертежа, падения у прямых m и n направленные в противоположные стороны: пад.D.