Доверительный интервал. Доверительная вероятность

Если значение испытываемого параметра оценивается одним числом, то оно называется точечным. Но в большинстве задач нужно найти не только наиболее достоверное численное значение, но и оценить степень достоверности.

Нужно знать: какую ошибку вызывает замена истинного параметра а его точечной оценкой 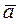; с какой степенью уверенности можно ожидать, что эти ошибки не превысят известные заранее установленные пределы.

Для этой цели в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.

Если для параметра а получена из опыта несмещенная оценка 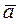, и поставлена задача оценить возможную при этом ошибку, то необходимо назначить некоторую достаточно большую вероятность β (например β = 0,9; 0,95; 0,99 и т.д.), такую, что событие с вероятностью β можно было бы считать практически достоверным.

В этом случае можно найти такое значение ε для которого P(| 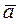- a| < ε) = β.

Рис. 7.1. Схема доверительного интервала.

В этом случае диапазон практически возможных ошибок, возникающих при замене а на 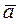не будет превышать ± ε. Большие по абсолютной величине ошибки будут появляться только с малой вероятностью α = 1 – β. Событие противоположное и неизвестное с вероятностью β будет попадать в интервал I_β = ( 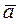- ε; + ε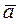). Вероятность β можно толковать, как вероятность того, что случайный интервал I_β накроет точку а (рис. 7.1).

Вероятность β принято называть доверительной вероятностью, а интервал I_β принято называть доверительным интервалом. На рис. 7.1 рассматривается симметричный доверительный интервал. В общем случае это требование не является обязательным.

Границы интервала а₁ = 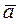- ε и a₂ = 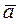+ ε, называются доверительными границами.

Доверительный интервал значений параметра a можно рассматривать как интервал значений a, совместных с опытными данными и не противоречащих им.

Выбирая доверительную вероятность β, близкую к единице, мы хотим иметь уверенность в том, что событие с такой вероятностью произойдет при осуществлении определенного комплекса условий.

Это равносильно тому, что противоположное событие не произойдет, что мы пренебрегаем вероятностью события, равною α = 1 – β. Укажем, что назначение границы а пренебрежимо малых вероятностей не являются математической задачей. Назначение такой границы находится вне теории вероятностей и определяется в каждой области степенью ответственности и характером решаемых задач.

Существуют специальные правила назначения границы пренебрежимо малых вероятностей. Например, такие случайные факторы, как уровень паводковых вод в реке или величина расхода воды в ней, могут привести к разрушению гидротехнических сооружений.

Но установление слишком большого запаса прочности приводит к неоправданному и большому удорожанию стоимости строительства.

Для сооружений особо капитальных (основные постоянные сооружения гидроэлектростанций мощностью более 250 тыс. квт с выработкой электроэнергии более 1 млрд. квт-ч в год) пренебрежимо малыми вероятностями считаются а = 0,001 при нормальных условиях эксплуатации и а = 0,0001 — при чрезвычайных. Для сооружений обычной капитальности назначают а = 0,002 или а = 0,005 в зависимости от условий эксплуатации.

Поясним, что здесь пренебрежение возможностью появления события с вероятностью в 0,001 означает риск разрушения один раз в 1000 лет.