Оценка вероятности по частоте
При испытаниях часто приходится оценивать неизвестную вероятность Р события А по его частоте 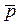 в «n» независимых опытах.
в «n» независимых опытах.
В общем случае, если в «п» проведенных опытах обозначить появление события А единицей, а непоявление события — нулем, то эмпирическая вероятность будет равна
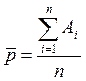
Математическое ожидание данной величины равно: М[ 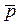 ] = р, а ее дисперсия: D[
] = р, а ее дисперсия: D[ 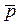 ] = pq/n, где q = 1 – p.
] = pq/n, где q = 1 – p.
В теории вероятностей доказывается, что эта дисперсия является минимально возможной, означающей, что оценка 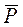 является эффективной.
является эффективной.
Доверительный интервал для вероятности 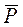 будет равен Iβ(
будет равен Iβ( 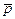 ) = (p1; p2),
) = (p1; p2),
где
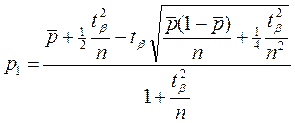
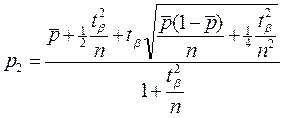
При n → ∞ величины 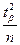 → 0 и
→ 0 и 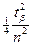 → 0, поэтому формулы в пределе принимают вид
→ 0, поэтому формулы в пределе принимают вид
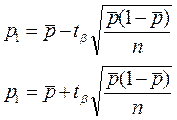
Формулами можно пользоваться при достаточно больших п (порядка сотен опытов) и когда вероятность р не слишком велика (когда величины пр и nq порядка 10 и более).
При малом числе опытом, а также в том случае, когда вероятность рочень велика или очень мала формулами для построения доверительного интервала пользоваться нельзя, т. к. они получены с рядом допущений.
В этом случае доверительный интервал строят из точного закона распределения частоты каковым является биномиальное распределение, для которого
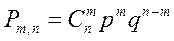
где Рт,п — вероятность появления т событий в п опытах, 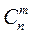 —число т сочетаний в n опытах. Частота
—число т сочетаний в n опытах. Частота 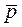 равна
равна 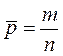 .
.
Значение доверительного интервала в этих случаях лучше не вычислять, а находить по специальным графикам. На рис. 7.2 приведен такой график для доверительной вероятности β = 0,9. В справочной литературе существуют таблицыp1 и р2 для различных β.
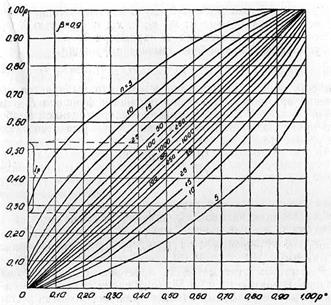
Рис. 7.2. Номограмма для определения p1; p2 при доверительной вероятности. β = 0.9.
Дата добавления: 2015-10-05; просмотров: 1193;
