Метод Байеса
Среди методов технической диагностики метод, основанный на обобщенной формуле Бaйeca, занимает особое место благодаря простоте и эффективности.
Разумеется, метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако в случаях, когда объем статистических данных позволяет применить метод Байеса, его целесообразно использовать как один из наиболее надежных и эффективных методов.
Основы метода. Метод основан на простой формуле Байеса. Если имеется диагноз Di и простой признак kj, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния Di и признака kj)
P (Dikj) = P (Di) P (kj/Di) = P (kj) P (Di/kj). (5.4)
Из этого равенства вытекает формула Байеса (см. гл. 11)
P(Di/kj) = P(Di) P(ki/Di)/P(kj) (5.5)
Очень важно определить точный смысл всех входящих в эту формулу величин.
P(Di) —вероятность диагнозаDi, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у Ni объектов имелось состояние Di, то
P(Di) = Ni/N. (5.6)
P (kj/Di) —вероятность появления признакаkjу объектов с состоянием Di. Если среди Ni объектов, имеющих диагнозDi, у Nij проявился признак kj, то
P(kj/Di) = Nij/Ni. (5.7)
P(kj) —вероятность появления признакаkj во всех объектахнезависимо от состояния (диагноза)объекта. Пусть изобщего числа N объектов признакkj был обнаружену Nj объектов, тогда
P(kj) = Nj/N. (5.8)
Для установления диагноза специальное вычисление P(kj)не требуется. Как будет ясно из дальнейшего,значения P(Di)и P (kj/Di),известные для всех возможных состояний, определяют величину P (kj).
Вравенстве (3.2) P (Di/kj)—вероятность диагноза Di послетого, как сталоизвестно наличие у рассматриваемого объекта признака kj (апостериорная вероятность диагноза).
Обобщенная формула Байеса.Эта формула относится к случаю, когда обследование проводится по комплексу признаков К,включающему признаки k1, k2, ..., kv.Каждый из признаков kj имеет mj разрядов (kjl, kj2, ..., kjs, ..., 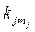 ). В результате обследования становитсяизвестной реализация признака
). В результате обследования становитсяизвестной реализация признака
kj*= kjs (5.9)
и всего комплекса признаков K*. Индекс *,как и раньше, означаетконкретное значение (реализацию) признака. Формула Байеса для комплексапризнаков имеет вид
P(Di/К*)= P(Di)P(К*/Di)/P(К*)(i = 1, 2, ..., n), (5.10)
где P (Di/К*) —вероятность диагноза Di после того, какстали известны результаты обследования по комплексу признаков К,P (Di) —предварительная вероятность диагноза Di (по предшествующей статистике).
Формула (5.10) относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний ипотому
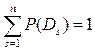 (5.11)
(5.11)
В практических задачах нередко допускается возможность существования нескольких состояний А1, ..., Аr, причем некоторые из них могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов Di следует рассматривать отдельные состояния D1 = А1, ..., Dr = Аr и их комбинации Dr+1 = А1 ^ А2, … и т. п.
Перейдем к определению P (К*/Di). Если комплекс признаков состоит из v признаков, то
P(К*/Di) = P(k1*/Di)P (k2*/k1*Di)...P (kv*/kl*...k*v-1Di), (5.12)
где kj* =kjs —разряд признака, выявившийся в результате обследования. Для диагностически независимых признаков
P (К*/Di) = P (k1*/Di) P (k2*/Di)... P (kv*/Di). (5.13)
В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними.
Вероятность появления комплекса признаковК*
P(К*)= 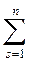 P(Ds)P(К*/Ds).(5.14)
P(Ds)P(К*/Ds).(5.14)
Обобщенная формула Байеса может быть записана так:
P(Di/K*) 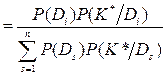 (5.15)
(5.15)
где P (К*/Di)определяется равенством (5.12) или (5.13). Изсоотношения (5.15) вытекает
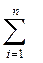 P(Di/К*)=l, (5.16)
P(Di/К*)=l, (5.16)
что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация одновременно двух диагнозов невозможна.
Следует обратить внимание на то, что знаменатель формулы Байеса для всех диагнозов одинаков. Это позволяет сначала определить вероятности совместного появления i-гo диагноза и данной реализации комплекса признаков
P(DiК*) = P(Di)P(К*/Di) (5.17)
и затем апостериорную вероятность диагноза
P (Di/К*) = P(DiК*)/ 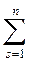 P(DsК*). (5.18)
P(DsК*). (5.18)
Отметим, что иногда целесообразно использовать предварительное логарифмирование формулы (5.15), так как выражение (5.13) содержит произведения малых величин.
Если реализация некоторого комплекса признаков К* является детерминирующей для диагноза Dp, то этот комплекс не встречается при других диагнозах:

Тогда, в силу равенства (5.15)
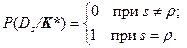 (5.19)
(5.19)
Таким образом, детерминистская логика установления диагноза является частным случаем вероятностной логики. Формула Байеса может использоваться и в том случае, когда часть признаков имеет дискретное распределение, а другая часть — непрерывное. Для непрерывного распределения используются плотности распределения. Однако в расчетном плане указанное различие признаков несущественно, если задание непрерывной кривой осуществляется с помощью совокупности дискретных значений.
Диагностическая матрица. Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу (табл. 5.1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков при различных диагнозах.
Таблица 5.1
Диагностическая матрица в методе Байеса
| Диагноз Di | Признак kj | P(Di) | ||||||||||
| k1 | k2 | k3 | ||||||||||
| P(k11/Di) | P(k12/Di) | P(k13/Di) | P(k21/Di) | P(k22/Di) | P(k23/Di) | P(k24/Di) | P(k31/Di) | P(k32/Di) | ||||
| D1 | 0,8 | 0,2 | 0,1 | 0,1 | 0,6 | 0,2 | 0,2 | 0,8 | 0,3 | |||
| D2 | 0,1 | 0,7 | 0,2 | 0,3 | 0,7 | 0,1 | 0,9 | 0,1 | ||||
| … | … | … | … | … | … | … | … | … | … | … | ||
Если признаки двухразрядные (простые признаки «да — нет»), то в таблице достаточно указать вероятность появления признака Р (ki/Di). Вероятность отсутствия признака Р ( 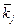 /D,-) = 1 - Р (ki/Di).
/D,-) = 1 - Р (ki/Di).
Однако более удобно использовать единообразную форму, полагая, например, для двухразрядного признака Р (kj/Di) = Р (ki1/Di); Р ( 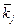 /D,) = Р (ki2 /Di).
/D,) = Р (ki2 /Di).
Отметим, что 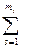 P(kjs/Di) = 1, где т, — число разрядов признака kj. Сумма вероятностей всех возможных реализаций признака равна единице.
P(kjs/Di) = 1, где т, — число разрядов признака kj. Сумма вероятностей всех возможных реализаций признака равна единице.
В диагностическую матрицу включены априорные вероятности диагнозов. Процесс обучения в методе Байеса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти ЭВМ следует хранить не только значения P(kjs/Di), но и следующие величины: N — общее число объектов, использованных для составления диагностической матрицы; Ni — число объектов с диагнозом Di; Nij — число объектов с диагнозом Di, обследованных по признаку kj. Если поступает новый объект с диагнозом Dμ, то проводится корректировка прежних априорных вероятностей диагнозов следующим образом:
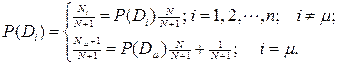 (5.20)
(5.20)
Далее вводятся поправки к вероятностям признаков. Пусть у нового объекта с диагнозом Dμ выявлен разряд r признака kj. Тогда для дальнейшей диагностики принимаются новые значения вероятности интервалов признака kj при диагнозе Dμ:
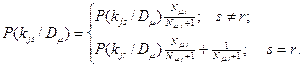 (5.21)
(5.21)
Условные вероятности признаков при других диагнозах корректировки не требуют.
Пример.Поясним метод Байеса. Пусть при наблюдении за газотурбинным двигателем проверяются два признака: k1— повышение температуры газа за турбиной более чем на 50 °С и k2 — увеличение времени выхода на максимальную частоту вращения более чем на 5 с. Предположим, что для данного типа двигателей появление этих признаков связано либо с неисправностью топливного регулятора (состояние D1,), либо с увеличением радиального зазора в турбине (состояние D2).
При нормальном состоянии двигателя (состояние D3)признак k1не наблюдается, а признак k2наблюдается в 5% случаев. На основании статистических данных известно, что 80% двигателей вырабатывают ресурс в нормальном состоянии, 5% двигателей имеют состояние D1и 15% - состояние D2. Известно также, что признак k1встречается при состоянии D1в 20% , а при состоянии D2 в 40% случаев; признак k2 при состоянии D1встречается в 30%, а при состоянии D2 - в 50% случаев. Сведем эти данные в диагностическую таблицу (табл. 5.2).
Найдем сначала вероятности состояний двигателя, когда обнаружены оба признака k1и k2. Для этого, считая признаки независимыми, применим формулу (5.15).
Вероятность состояния
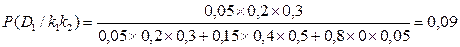
Аналогично получим Р (D2/k1k2) = 0,91; Р (D3/k1k2) = 0.
Определим вероятность состояний двигателя, если обследование показало, что повышение температуры не наблюдается (признак k1), но увеличивается время выхода на максимальную частоту вращения (признак k2 наблюдается). Отсутствие признака k1 есть признак наличия 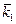 (противоположное событие), причем Р (
(противоположное событие), причем Р ( 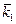 /Di) = 1 - Р (k1/Di).
/Di) = 1 - Р (k1/Di).
Для расчета применяют также формулу (5.15), но значение Р (k1/Di) в диагностической таблице заменяют на Р ( 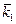 /Di). В этом случае
/Di). В этом случае
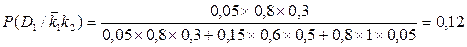
и аналогично Р (D2/  k2) = 0,46; Р (D3/
k2) = 0,46; Р (D3/  k2) = 0,41. Вычислим вероятности состояний в том случае, когда оба признака отсутствуют. Аналогично предыдущему получим
k2) = 0,41. Вычислим вероятности состояний в том случае, когда оба признака отсутствуют. Аналогично предыдущему получим
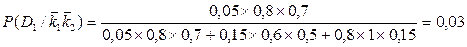

Отметим, что вероятности состояний D1 и D2 отличны от нуля, так как рассматриваемые признаки не являются для них детерминирующими. Из проведенных расчетов можно установить, что при наличии признаков k1 и k2 в двигателе с вероятностью 0,91 имеется состояние D1, т.е. увеличение радиального зазора. При отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0,92). При отсутствии признака k1 и наличии признака k2 вероятности состояний D2 и D3 примерно одинаковы (0,46 и 0,41) и для уточнения состояния двигателя требуется проведение дополнительных обследований.
Таблица 5.2
Вероятности признаков и априорные вероятности состояний
| Di | P(k1/Di) | P(k2/Di) | P(Di) |
| D1 | 0,2 | 0,3 | 0,05 |
| D2 | 0,4 | 0,5 | 0,15 |
| D3 | 0,0 | 0,05 | 0,80 |
Решающее правило— правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса объект с комплексом признаков К* относится к диагнозу с наибольшей (апостериорной) вероятностью
K* 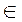 Di,если P(Di/K*) > P(Dj/K*) (j = 1, 2,..., n; i ≠ j). (5.22)
Di,если P(Di/K*) > P(Dj/K*) (j = 1, 2,..., n; i ≠ j). (5.22)
Символ 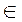 , применяемый в функциональном анализе, означает принадлежность множеству. Условие (5.22) указывает, что объект, обладающий данной реализацией комплекса признаков К* или, короче, реализация К* принадлежит диагнозу (состоянию) Di. Правило (5.22) обычно уточняется введением порогового значения для вероятности диагноза:
, применяемый в функциональном анализе, означает принадлежность множеству. Условие (5.22) указывает, что объект, обладающий данной реализацией комплекса признаков К* или, короче, реализация К* принадлежит диагнозу (состоянию) Di. Правило (5.22) обычно уточняется введением порогового значения для вероятности диагноза:
P (Di/K*) ≥ Pi, (5.23)
где Pi. — заранее выбранный уровень распознавания для диагноза Di. При этом вероятность ближайшего конкурирующего диагноза не выше 1 – Pi. Обычно принимается Pi ≥ 0,9. При условии
P(Di/K*)<Pi (5.24)
решение о диагнозе не принимается (отказ от распознавания) и требуется поступление дополнительной информации.
Процесс принятия решения в методе Байеса при расчете на ЭВМ происходит достаточно быстро. Например, постановка диагноза для 24 состояний при 80 многоразрядных признаках занимает на ЭВМ с быстродействием 10 - 20 тысяч операций в секунду всего несколько минут.
Как указывалось, методу Байеса присущи некоторые недостатки, например погрешности при распознавании редких диагнозов. При практических расчетах целесообразно провести диагностику и для случая равновероятностных диагнозов, положив
P(Di) = l / n (5.25)
Тогда наибольшим значением апостериорной вероятности будет обладать диагноз Di, для которого Р (K*/Di) максимальна:
K* 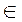 Di,если P(K*/Di) > P(K*/Dj) (j = 1, 2,..., n; i ≠ j). (5.26)
Di,если P(K*/Di) > P(K*/Dj) (j = 1, 2,..., n; i ≠ j). (5.26)
Иными словами, устанавливается диагноз Di если данная совокупность признаков чаще встречается при диагнозе Di, чем при других диагнозах. Такое решающее правило соответствует методу максимального правдоподобия. Из предыдущего вытекает, что этот метод является частным случаем метода Байеса при одинаковых априорных вероятностях диагнозов. В методе максимального правдоподобия «частые» и «редкие» диагнозы равноправны.
Для надежности распознавания условие (5.26) должно быть дополнено пороговым значением
P(K*/Di) ≥ Pi, (5.27)
где Pi — заранее выбранный уровень распознавания для диагноза Di.
Дата добавления: 2015-10-05; просмотров: 1246;
