Лекция 9. Свойства матрицы проводимости:
Свойства матрицы проводимости:
1. При отсутствии в сети трансформаторов с комплексными коэффициен-тами трансформации, матрица является симметричной, то есть выполняется принцип взаимности Yij = Yji ;
2. Матрица является слабозаполненной, так как содержит большое коли-чество нулевых элементов. Причина - если узлы не связаны между собой, то их взаимная проводимость равна нулю (yij = 0), а в реальных сетях каждый узел связан с небольшим числом узлов;
Свойства 1 и 2 используются для компактного хранения матрицы проводимостей в памяти ЭВМ (хранятся только ненулевые элементы и их координаты). Количество собственных проводимостей равно количеству узлов в сети, количество взаимных проводимостей равно числу ветвей ( с учетом симметричности матрицы).
3. Матрица проводимостей неособенная, то есть её определитель 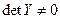 , следовательно она имеет обратную матрицу.
, следовательно она имеет обратную матрицу.
Пример: Составить матрицу проводимостей для схемы
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | y11 | -y12 | -y14 | -y17 | ||||
| 2 | -y21 | y22 | -y23 | |||||
| 3 | -y32 | y33 | -y35 | |||||
| 4 | -y41 | y44 | -y45 | |||||
| 5 | -y53 | -y54 | y55 | -y56 | -y58 | |||
| 6 | -y65 | y66 | -y68 | |||||
| 7 | -y71 | y77 | -y78 | |||||
| 8 | -y85 | -y86 | -y87 | y88 |

Собственные проводимости узлов схемы:
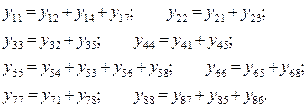
В памяти ЭВМ запоминается верхняя половина матрицы (её ненулевые элементы).
Система уравнений (4) – это система уравнений узловых напряжений в форме баланса токов, записана для всех узлов сети и содержит n уравнений относительно n неизвестных напряжений в узлах. В таком виде она не может дать искомое решение для всех комплексных напряжений, так как:
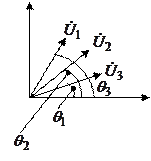 1. Если
1. Если 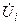 является решением ( i= 1 … n ) системы уравнений, то
является решением ( i= 1 … n ) системы уравнений, то 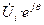 тоже является решением, так как это соответствует пово-роту всех векторов напряжения на угол
тоже является решением, так как это соответствует пово-роту всех векторов напряжения на угол 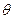 . Множитель
. Множитель 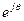 входит во все решения и может быть сокращен. Задавая разные значения
входит во все решения и может быть сокращен. Задавая разные значения 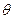 можем получить множество решений системы уравнений;
можем получить множество решений системы уравнений;
2. Если в узлах не задать (не зафиксировать) ни од-ного напряжения, то можно получить решение, не имею-щее практического смысла (например, отрицательные напряжения в узлах, либо напряжения не соответствую-щие своему классу напряжений и т. д.). При этом баланс токов в узлах будет соблюдаться.
Решение этой проблемы: в сети выбирают один (или несколько) узлов, в которых фиксируют модуль и угол напряжения. Это узлы с фиксацией векто-ра напряжения (ФВ). Такие узлы называются базисными или опорными по напряжению 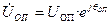 = const. В сети должен быть хотя бы один такой узел. Во всех остальных узлах схемы напряжения рассчитывается относи-тельно опорного. В схеме им соответствуют, как правило шины электростан-ций или мощных подстанций. Как правило опорный узел по напряжению сов-падает с балансирующим по мощности. Для упрощения расчетов часто задают
= const. В сети должен быть хотя бы один такой узел. Во всех остальных узлах схемы напряжения рассчитывается относи-тельно опорного. В схеме им соответствуют, как правило шины электростан-ций или мощных подстанций. Как правило опорный узел по напряжению сов-падает с балансирующим по мощности. Для упрощения расчетов часто задают 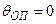 .
.
Задание в некоторых узлах сети векторов напряжения, т.е. выделение в схеме сети опорных узлов с ФВ (которые совпадают с балансирующими) приводит к уменьшению числа неизвестных в системе уравнений (4) и необхо-димости исключения из неё уравнений, соответствующих этим узлам (т.к. уменьшается число неизвестных напряжений).
Пример:
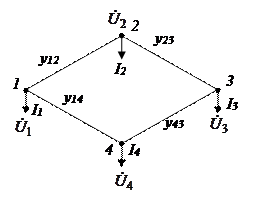 Запишем для схемы систему уравнений вида (4):
Запишем для схемы систему уравнений вида (4):
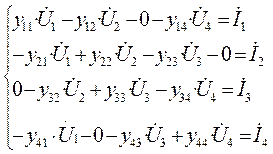
Система уравнений в матричной форме:
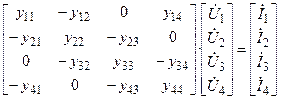
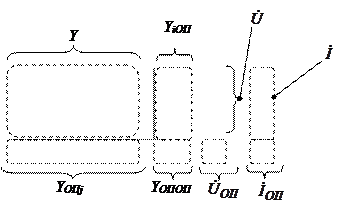 |
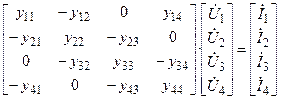
В качестве спорного узла выберем узел 4. Напряжение 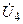 в нём задано. Нужно исключить из системы уравнение, соответствующее опорному узлу – уравнение 4. Это соответствует четвёртой строке в матрице и в вектор – столб-це. В матрице выделим столбец и строку, соответствующие опорному узлу – номер 4 – они содержат его взаимные проводимости с другими узлами схемы.
в нём задано. Нужно исключить из системы уравнение, соответствующее опорному узлу – уравнение 4. Это соответствует четвёртой строке в матрице и в вектор – столб-це. В матрице выделим столбец и строку, соответствующие опорному узлу – номер 4 – они содержат его взаимные проводимости с другими узлами схемы.
В матрице и векторах выделяются блоки и субвектора:
YiОП – вектор – столбец взаимных проводимостей между узлами сети и опорным узлом;
YОПj – вектор – строка взаимных проводимостей между опорным узлом и другими узлами сети;
Y – неполная матрица проводимостей, получаемая из полной удалением строк и столбцов соответствующих опорным узлам;
YОПОП – собственная проводимость опорного узла;
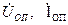 - заданные напряжения в опорных узлах и токи в них;
- заданные напряжения в опорных узлах и токи в них;
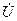 - вектор искомых напряжений в узлах сети;
- вектор искомых напряжений в узлах сети;
 - вектор заданных токов в узлах сети.
- вектор заданных токов в узлах сети.
С учётом этого в блочной форме система уравнений может быть записана:
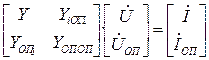 .
.
Удаляем элементы (блоки), соответствующие уравнениям опорных узлов - YОПj, YОПОП, IОП. Тогда по правилам умножения блочных матриц получаем:
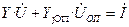 .
.
Переносим известные величины в правую часть:
.
Это система уравнений установившегося режима в матричной форме.
Это уравнения в виде баланса токов. Линейные уравнения.
В результате преобразований можно получить другой вид этой системы урав-нений:
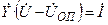 .
.
При задании в узлах сети нелинейных источников тока (генераторы или нагрузки с постоянной мощностью), установившийся режим описывается нели-нейными уравнениями:
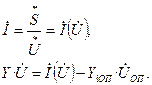
Эти уравнения – нелинейные уравнения установившегося режима в форме баланса тока. При задании в узлах нелинейных источников тока установив-шийся режим сети можно описать, также, нелинейными уравнениями в форме баланса мощности.
 В результате преобразований уравнения баланса мощности в матричной форме будут иметь вид:
В результате преобразований уравнения баланса мощности в матричной форме будут иметь вид:
|
Здесь 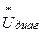 - диагональная матрица, на главной диагонали которой рас-
- диагональная матрица, на главной диагонали которой рас-
положены сопряженные комплексы напряжений;
S - заданные мощности в узлах.
Дата добавления: 2015-10-05; просмотров: 3345;

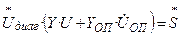 .
.