Матричная форма записи уравнений установившегося режима
Уравнения установившегося режима в форме баланса токов:
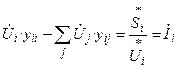 , (1)
, (1)
где 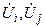 - напряжение в рассматриваемом i – м узле и напряжения в смежных узлах j . Это неизвестные величины;
- напряжение в рассматриваемом i – м узле и напряжения в смежных узлах j . Это неизвестные величины;
yij – взаимная проводимость узлов
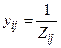 ;
;
yij – собственная проводимость i – го узла
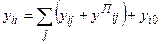 (2)
(2)
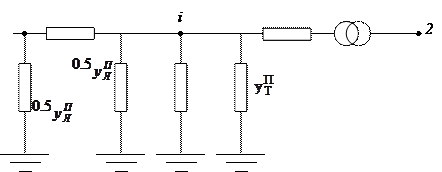
уі0
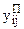 - поперечная проводимость участков подходящих к i – у узлу:
- поперечная проводимость участков подходящих к i – у узлу:

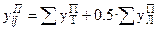 (3)
(3)
 |
Поперечные проводимости транс- Поперечная проводимость
формирующих участков линии
yi0 – собственная проводимость устройств, подключенных непосредст-венно в i – м узле;
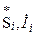 - заданные мощность или ток.
- заданные мощность или ток.
Уравнение (1) сформировано на основе метода узловых потенциалов, за-писано для одного і – го узла сети. Для схемы, состоящий из n узлов записы-вается n таких уравнений с n комплексными неизвестными.
Запишем систему уравнений вида (1) для абстрактной схемы электрической сети, состоящей из n узлов:
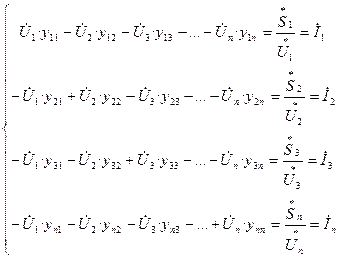
(4)
Эта система уравнений описывает режим роботы ЭС в целом. Запишем эту систему в матричной форме:
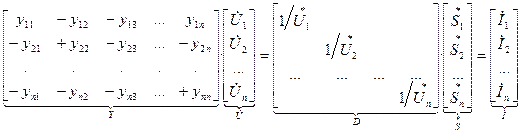 (5)
(5)
С учетом обозначений система (5) примет вид:
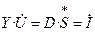 . (6)
. (6)
Здесь Y – матрица коэффициентов при неизвестных – матрица собственных
и взаимных проводимостей (матрица проводимостей);
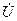 - вектор неизвестных – вектор напряжений;
- вектор неизвестных – вектор напряжений;
D – диагональная матрица, на главной диагонали которой расположены
величины, обратные сопряженному комплексу напряжений в узлах.
Остальные элементы матрицы - нули;
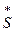 - вектор сопряженных комплексов заданных мощностей в узлах;
- вектор сопряженных комплексов заданных мощностей в узлах;
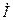 - вектор заданных токов в узлах.
- вектор заданных токов в узлах.
Матрица собственных и взаимных проводимостей Y
Ее элементами являются проводимости узлов и участков. На главной диа-гонали расположены собственные проводимости узлов, определяемые по фор-муле (2). Вне главной диагонали - взаимные проводимости узлов, взятые с об-ратным знаком. Матрица квадратная, симметричная.
Если узлы сети соединены между собой, то их взаимная проводимость отлична от нуля ( Yij = 1/Zij). Если узлы между собой не связаны, то Yij = 0.
Т.к. реальные сети имеют большое количество узлов, а каждый узел имеет не-большое число связей с другими узлами (до 10), то строки матрицы и матрица в целом содержат большое количество нулевых элементов (матрица слабоза-полненная или разреженная).
Каждая строка матрицы соответствует одному узлу сети и его связям.
По структуре матрицы проводимостей можно определить схему сети и ее параметры. То есть матрица проводимостей представляет собой модель схемы электрической сети.
Пример: Дана матрица проводимостей. По её структуре определим схему
сети:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | x | x | x | ||
| 2 | x | x | |||
| 3 | x | x | |||
| 4 | x | x | x | x | |
| 5 | x | x |
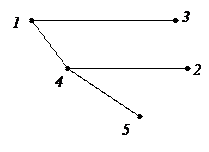
| |
Уравнения (5) и (6) представляют собой математическую модель режи-ма работы ЭС в общем виде.
Дата добавления: 2015-10-05; просмотров: 1031;
