Лекция 8. В практических расчетах комплексные уравнения (9) и (11) часто исполь-зуются в преобразованном виде

В практических расчетах комплексные уравнения (9) и (11) часто исполь-зуются в преобразованном виде. Комплексные величины в их составе пред-ставляются в виде действительных и мнимых составляющих. В результате, комплексное уравнение распадается на два действительных уравнения.

Преобразуем уравнение (11), представив неизвестные напряжения (комп-лексные величины) U_i ,U_j в прямоугольных координатах:

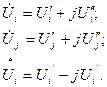
Проводимости тоже представим в виде составляющих:

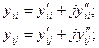(12)

Мощность: ;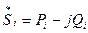

Подставим эти значения в (11):

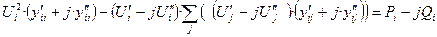
Выполняем преобразование: раскрываем скобки, группируем, разделяем действительную и мнимую части уравнения. Получаем два действительных

уравнения установившегося режима в форме баланса мощностей, записанных в прямоугольных координатах:

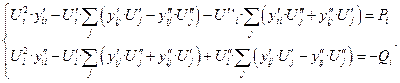(13)

Неизвестные величины в них - составляющие напряжений U_i^’, U_i^”, U_j^’, U_j^”.

Уравнение (13) описывает баланс активной и реактивной мощности в одном i – м узле сети. Для сети, состоящей из n узлов нужно записать 2n таких урав-нений. Неизвестными являются составляющие напряжения .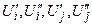

Представим уравнение (11) в полярных координатах. Для этого комплексы неизвестных напряжений запишем в соответствии с формулой Эйлера:

.

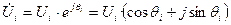Здесь U_i – модуль, 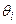- фаза напряжения .

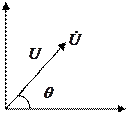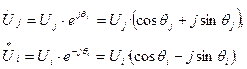(14)

Подставим (14) в (11) учетом того, что

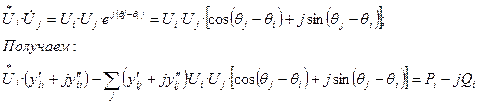(15)

Преобразуем уравнение (15): раскрываем скобки, группируем, разделя-ем действительные и мнимые части, меняем местами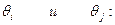

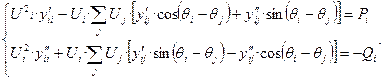(16)

Это уравнение установившегося режима в форме баланса мощности,

записанное в полярных координатах. Неизвестные величины в нём - модули напряжений 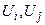и фазы напряжений .

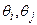Это два действительных уравнения, записанные для одного i-го узла схемы. Определяют баланс активной и реактивной мощности в нем.

Существуют и другие формы записи уравнений установившегося режима.

Пример:

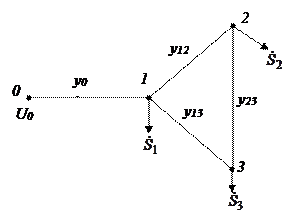
Составить уравнения в форме баланса токов для каждого из узлов сети

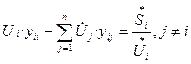
Составим уравнение для первого узла.

Для него i=1; j=0,2,3; n=3;

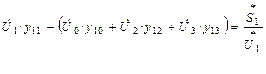
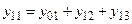- собственная проводимость 1 – го узла.

Для узла 0: i=0; j=1; n=1;

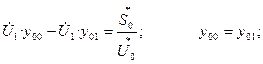
Для узла 2: i=2; j=1,3; n=2;

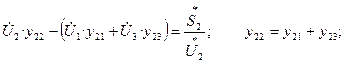
Для узла 3: i=3; j=1,2; n=2;

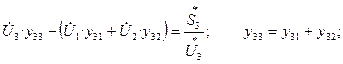
Уравнения в форме баланса мощностей можно получить, если умножить каждое из полученных уравнений на сопряженный комплекс соответствующе-го напряжения.

Запишем уравнение для 1 – го узла в прямоугольных координатах:

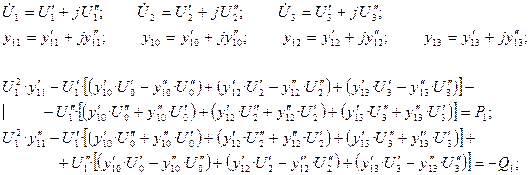
Для узлов 2 и 3 уравнения в прямоугольных координатах записать самостоятельно.

Уравнения для 1-го узла в полярных координатах:

i=1; j=0,2,3; n=3;

Используем формулу (16):