Тема 10. Механика жидкости. Уравнение Бернулли

Гидростатика. Для несжимаемой жидкости ее плотность не зависит от давления. При поперечном сечении S столба жидкости плотностью r ивысотой h давление жидкости р на нижнее основание:

.

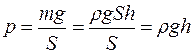Давление 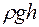называетсягидростатическим давлением.

Плотность тела в точке записывается как 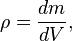тогда масса неоднородного тела (тела с плотностью, зависящей от места)

рассчитывается как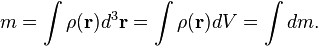

Как и в случае абсолютно твердого тела, применимость представления об абсолютно несжимаемой жидкости определяется не столько свойствами самой жидкости, сколько условиями, в которых она находится. Например, при изучении распространения звуковых волн в жидкости всегда необходимо учитывать ее сжимаемость, в то время как при изучении движения потоков не только жидкость, но и газ часто можно рассматривать как несжимаемые.

Гидродинамика. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 9). Линии тока проводятся таким образом, чтобы их густота характеризовала величину скорости: густота больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее.

Часть жидкости, ограниченную линиями тока, называют трубкой тока (рис. 10). Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

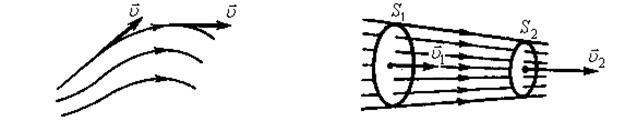
Рис. 9 Рис. 10

Уравнение неразрывности струи для несжимаемой жидкости.Рассмотрим какую-либо трубку тока. Выберем два ее сечения S₁ и S₂ , перпен­дикулярные направлению скорости (рис. 10).

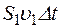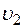За время Dt через сечение S₁ проходит объем жидкости ,где – скорость течения жидкости в месте сечения S₁ , а через сечение S₂ за тоже время Dt пройдет объем жидкости , где – скорость течения жидкости в месте сечения S₂ . Если жидкость несжимаемая, то через сечение S₂ пройдет такой же объем жидкости, как и через сечение S₁ , т. е.

.

Так как положения сечений S₁ и S₂ выбраны произвольно, то отсюда следует, что вдоль данной трубки тока 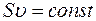. Это соотношение называетсяуравнением неразрывности струи для несжимаемой жидкости.

Уравнение Бернулли. Бернулли рассмотрел изменения гидродинамических параметров вдоль произвольно выбранной трубки тока стационарно текущей жидкости плотностью r (рис. 11).

Рис. 11

В месте сечения трубки тока S₁ скорость течения жидкости , давление p₁ и высота, на которой это сечение расположено относительно выбранного уровня отсчета, h₁. Аналогично, в месте сечения трубки тока S₂ скорость течения жидкости 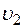, давление p₂ и высота расположения этого сечения над тем же уровнем отсчета h₂ .

Бернулли установил, что для любых двух сечений одной трубки тока несжимаемой жидкости выполняется равенство:

.

Так как положения сечений было выбрано произвольно, то для любой трубки тока несжимаемой жидкости гидродинамические параметры жидкости подчиняются следующему уравнению (уравнению Бернулли):

.

Для горизонтальной трубки тока (h = const) уравнение Бернулли принимает вид:

,

где величина 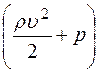называетсяполным давлением,

величина р называетсястатическим давлением,

величина называетсядинамическим давлением.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности струи следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление, наоборот, в местах сужения меньше.

Динамика движения реальной жидкости очень сложна. Для упрощения ее описания в некоторых случаях можно пренебречь силами внутреннего трения. Такую жидкость называют идеальной. При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, механическая энергия жидкости сохраняется. Уравнение Бернулли было выведено для достаточно узкой трубки тока и, строго говоря, справедливо, когда эта трубка тока сжимается в линию тока.

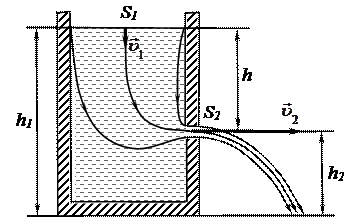Формула Торричелли.Формула Торричелли позволяет находить скорость истечения жидкости через малое отверстие в стенке или дне сосуда (рис. 12). Формула Торричелли следует из уравнения Бернулли.Если применить это уравнение для двух сечений S₁ и S₂ (S₁ на уровне h₁ cвободной поверхности жидкости в сосуде и S₂ на уровне отверстия h₂), то получим равенство: Рис.12

.

Так как давления р₁ и р₂ жидкости на уровнях первого и второго сечений равны атмосферному, то р₁=р₂ , а полученное соотношение примет вид:

.

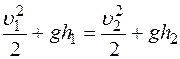Из уравнения неразрывности струи следует, что ,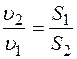

где S₁ и S₂ – площади поперечных сечений сосуда и отверстия.

Так как S₁>>S₂ ,то 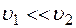и членом 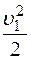можно пренебречь.

Тогда ,

откуда .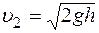

Это выражение получило название формулы Торричелли, где h – высота свободной поверхности жидкости в сосуде над уровнем отверстия.

Формула Торричелли справедлива только для идеальнойжидкости, то есть для жидкости, в которой отсутствует вязкость или внутреннее трение. Только в этом случае скорость истечения жидкости из малого отверстия такая же по величине, как и скорость тела, свободно падающего с высоты h.

Гидравли́ческий уда́р (гидроудар) — скачок давления в какой-либо системе, заполненной жидкостью, вызванный крайне быстрым изменением скорости потока этой жидкости за очень малый промежуток времени. Может возникать вследствие резкого закрытия или открытия задвижки. В первом случае гидроудар называют положительным, во втором - отрицательным. Опасен положительный гидроудар. При положительном гидроударе несжимаемую жидкость следует рассматривать как сжимаемую. Гидравлический удар способен вызывать образование продольных трещин в трубах, что может привести к их расколу, или повреждению других элементов трубопровода. Также гидроудары чрезвычайно опасны и для другого оборудования, такого как теплообменники, насосы и сосуды, работающие под давлением. Для предотвращения гидроударов, вызванных резкой переменой направления потока рабочей среды, на трубопроводах устанавливаются обратные клапаны.

Дании́л Берну́лли (Daniel Bernoulli; 29 января (8 февраля) 1700 — 17 марта 1782), швейцарский физик-универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).