Сложение взаимно перпендикулярных колебаний. Числом степеней свободы механической системы называется число независимых координат, необходимых для описания состояния этой системы

Числом степеней свободы механической системы называется число независимых координат, необходимых для описания состояния этой системы. Если колебательная система имеет больше чем одну степень свободы, то при колебаниях могут изменяться все координаты, которые соответствуют этим степеням свободы системы.

В качестве примера колебательной системы, имеющей две степени свободы, рассмотрим тяжелый шар, подвешенный на длинной тонкой нити (математический маятник). При определенных внешних воздействиях этот шар может совершать два колебания во взаимно перпендикулярных направлениях. Если возбудить одновременно оба колебания, то шар будет двигаться по некоторой сложной траектории, форма которой зависит от частот и разности фаз обеих колебаний.

Другая модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на рисунке. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.

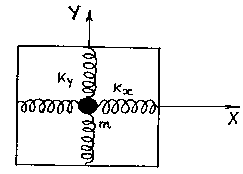
Рассмотрим сложение двух взаимно перпендикулярных гармонических колебаний одинаковой частоты ω. Пусть материальная точка участвует в двух колебаниях, которые совершаются вдоль координатных осей X и Y. Уравнения колебаний будут:

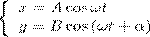
При разности фаз, равной 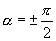.уравнением траектории является уравнение эллипса, приведенного к координатным осям:

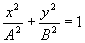
Полуоси эллипса равны соответствующим амплитудам колебаний. Если амплитуды А и В равны, эллипс превращается в окружность.