Сложение гармоническихколебаний одного направления и одинаековой частоты

Гармонические колебания одинакового направления и частоты удобно складывать, изобразив колебания в виде векторов на плоскости - графически.

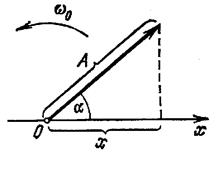1). Выберем некоторую направленную прямую - ось, вдоль которой будем откладывать колеблющуюся величину x .

2). Из взятой на оси некоторой точки О отложим направленный отрезок - вектор длины A, образующий с осью угол некоторый α .

3). Вращая вектор А вокруг точки О с угловой скоростью ω ₀ , получим, что проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени: проекция конца вектора будет перемещаться по оси x, принимая значения от - А до + A , а координата этой проекции будет изменяться со временем по закону

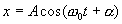
Схему, полученную таким методом представления колебаний, называют векторной диаграммой .

Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты

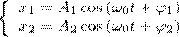
применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рисунок).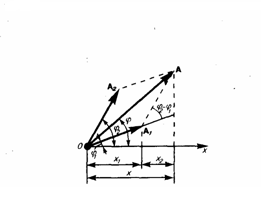

Taк как векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂ - φ₁) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет

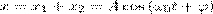(1)

В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями

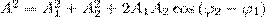
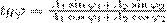
Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ₂ - φ₁) складываемых колебаний.

Исследуем выражение для амплитуды А в зависимости от разности фаз (φ₂ - φ₁):

1) φ₂ - φ₁ = ±2mπ (m = 0, 1, 2, ...), тогда A=A₁+A₂, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;

2) φ₂ - φ₁ = ±(2m+1)π (m = 0, 1, 2, ...), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.