Замена переменных в тройном интеграле (общая формулировка).
Теорема. Пусть функции
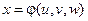 ,
, 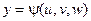 ,
, 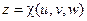
взаимно однозначно отображают область V в декартовых координатах х, у, z на область Ωв криволинейных координатах и, v, w. Пусть элемент объема ΔV области V переходит в элемент ΔΩ области Ω и пусть
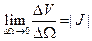
Тогда (для интегрируемой функции 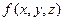 определенной на V)
определенной на V)
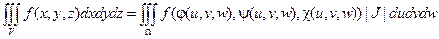
и
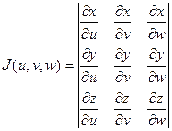
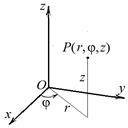 Цилиндрические координаты. Цилиндрические координаты точки связаны с прямоугольными декартовыми (при их стандартном взаимном расположении) соотношениями
Цилиндрические координаты. Цилиндрические координаты точки связаны с прямоугольными декартовыми (при их стандартном взаимном расположении) соотношениями
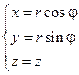
которые можно рассматривать как отображение замкнутой области
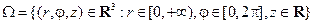
на Q = R3. Отметим, что данное отображение не является взаимно однозначным. Однако, как и в случае полярных координат на плоскости, формула перехода к криволинейным координатам остается верной в цилиндрических координатах.
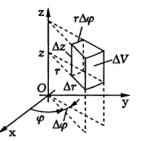 Координатными поверхностями в цилиндрической системе координат будут:
Координатными поверхностями в цилиндрической системе координат будут:
1) полуплоскости φ = const, проходящие через ось Oz;
2) цилиндрические поверхности r = const с образующими, параллельными оси Oz, и направляющими в виде концентрических окружностей с центром на этой оси, лежащих в плоскости, перпендикулярной оси Oz;
3) плоскости z = const, перпендикулярные оси Oz.
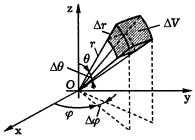
Якобиан отображения:
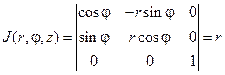
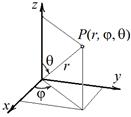
Сферические координаты.Сферические координаты r, φи θсвязаны с декартовыми координатами x, у, z (при стандартном взаимном расположении двух систем координат) соотношениями
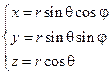
которые определяют отображение замкнутой области
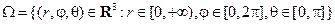
в замкнутую область Q = R3. Это отображение непрерывно дифференцируемо, но в Ω не является взаимно однозначным. Тем не менее формула перехода к криволинейным координатам, как и в случае полярных и цилиндрических координат, остается верной.
Напомним, что сферические координаты имеют следующий геометрический смысл:
1) величина r есть длина радиус-вектора OMточки М;
 2) величина φесть угол между проекцией ОМ1радиус-вектора OMна плоскость xOy и осью Ox;
2) величина φесть угол между проекцией ОМ1радиус-вектора OMна плоскость xOy и осью Ox;
3) величина θесть угол между вектором ОМи осью Oz.
Сферическим координатам отвечают следующие семейства координатных поверхностей:
1) концентрические сферы r = const с центром в точке О;
2) полуплоскости φ= const, проходящие через ось Oz и ограниченные этой осью;
3) круговые полуконусы θ = const с вершиной в точке О, осью симметрии которых является ось Оz.
Якобиан отображения:
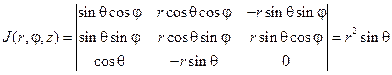
Замечание. Существует другой вариант сферической системы координат, в котором вместо угла θ используется угол ψ, который отсчитывается не от оси Oz, а от координатной плоскости хОу. В этом варианте областью изменения координаты ψявляется отрезок 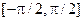 , а якобиан отображения, связывающего сферические и декартовы координаты, равен
, а якобиан отображения, связывающего сферические и декартовы координаты, равен 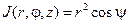 .
.
Применение кратных интегралов для вычисления центра масс и моментов инерции. Объем области трехмерного пространства OXYZ равен
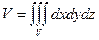
Масса тела, занимающего область V,
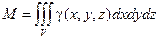
где 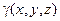 − плотность тела в точке
− плотность тела в точке 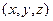 .
.
Статические моменты тела относительно координатных плоскостей
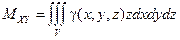 ,
, 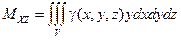
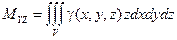
Координаты центра тяжести
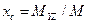 ,
, 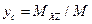 ,
, 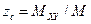
Моменты инерции относительно осей координат
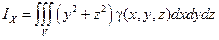 ,
, 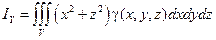
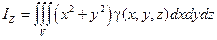
Пример1. Расставить пределы интегрирования в тройном интеграле
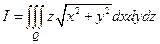
по замкнутой области Q, ограниченной плоскостями у = 0, z = 0, z = a и поверхностью 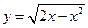 у. Вычислить этот интеграл, переходя к цилиндрическим координатам.
у. Вычислить этот интеграл, переходя к цилиндрическим координатам.
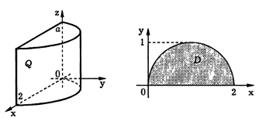
В декартовых координатах
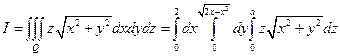
В координатах (x, y) 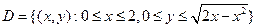 , а в цилиндрических:
, а в цилиндрических: 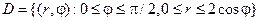 . Поэтому
. Поэтому
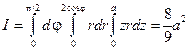
Пример 2. Вычислить объем V тела Q, ограниченного поверхностью 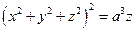 .
.
Тело можно описать с помощью неравенства 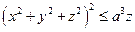 , которое в сферической системе координат является достаточно простым:
, которое в сферической системе координат является достаточно простым: 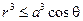 . Поскольку r ≥ 0, то
. Поскольку r ≥ 0, то 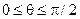 . Переменное φ вообще не входит в неравенство. Поэтому область изменения φмаксимальная:
. Переменное φ вообще не входит в неравенство. Поэтому область изменения φмаксимальная:
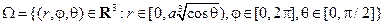
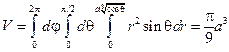
| <== предыдущая лекция | | | следующая лекция ==> |
| Примеры решения типовых задач. Пример 1. Составление формулы и диссоциация комплексного соединения, вычисление заряда комплексного иона | | | Градиент и его свойства. |
Дата добавления: 2015-10-05; просмотров: 2223;
