Переходный процесс электропривода с двигателем независимого возбуждения при из­менении магнитного потока

Обычно ДНВ работает при Ф=Ф_н если U=const или U=var. Необходимость ослабления по­тока возникает когда требуется получить скорость, превышающую основную (согласно тре­бованиям технологического процесса ). Если бы поток изменялся мгновенно, то в началь­ный момент времени имел бы место бросок тока и момента, как показано на рисунках w=f(I_a) и w=f(M) пунктиром . В действительности Ф изменяется во времени. Поэтому ток якоря и момент двигателя будут изменяться по т.н. динамическим характеристикам (кривая1). Для расчета переходного процесса пренебрегаем индуктивностью якоря L_Я т.к. она мала по сравнению с индуктивностью L_В обмотки возбуждения. Бросок тока и момента будет тем больше, чем быстрее темп изменения Ф. Для получения расчетного выражения воспользуемся уравнением равновесия ЭДС в якорной цепи и уравнением момента.

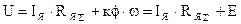
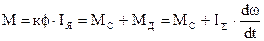
Выразим коэффициенты “k” через номинальные параметры. Коэффициенты ЭДС

;

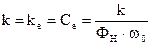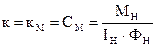
1) 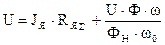; 2)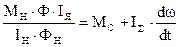

Определив из второго уравнения I_Я и подставив в первое, а также разделив полученное выражение на 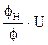, получим

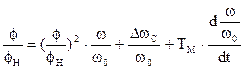или в относительных единицах

3) 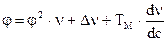, где ;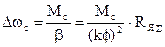

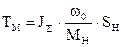
Это уравнение нелинейное и решить его непосредственно нельзя, т.к. f=f(t). При небольших пределах изменения Ф можно считать, что Ф изменяется по линейному закону, как показано на графике кривой намагничивания. Линейное изменение потока имеет место в случае, если 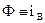, т.е. когда цепь машины не насыщена (здесь допускается некоторая погрешность). Закон изменения тока возбуждения при ненасыщенной магнитной цепи можно найти из уравнения равновесия ЭДС для цепи возбуждения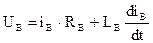

Отсюда 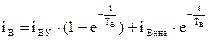, где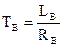

При 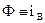закон изменения потока будет таким же 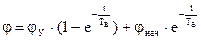. Это экспонента.

Для расчета строится кривая j=f(t) и разбивается на участки постоянной длительности. На каждом участке длительностью Dt поток j считается постоянным, равным среднему значению 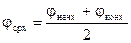. Аналогично скорость двигателя в течении Dt считаем постоянной и равной среднему значению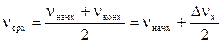

Подставив значения 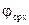и 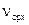в уравнение 3 , решаем его относительно

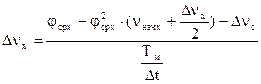
Окончательная расчетная формула имеет вид

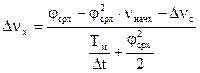
Расчет кривой скорости ведется с первого участка длительностью Dt, для которого известна 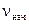и среднее значение потока 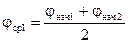. Приращение скорости на первом участке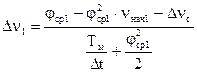

Начальная скорость на втором участке длительностью Dt равна скорости в конце первого участка, т.е. 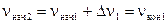. Аналогично определяется приращение скорости на втором участке и т.д. По рассчитанным приращениям строится кривая n=f(t), которая изображена на графике.

Для нахождения закона изменения тока J_Я в переходном режиме разделим обе части уравнения 1 на U

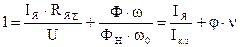отсюда

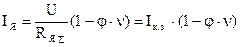
Конечное значение тока якоря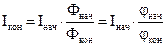

Поскольку значения j и n для каждого участка длительностью Dt известны, можно построить кривую J_Я=f(t). Примерный вид этой кривой при М_c = const приведен на рис.

Закон изменения момента находится аналогично согласно уравнению движения

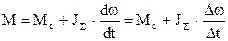
Если бросок тока при ослаблении f окажется недопустимым по условиям коммутации, изменение f следует осуществлять в несколько ступеней.

Расчет переходного процесса можно вести и в именованных величинах. Расчетное выражение для определения приращения скорости можно получить аналогично изложенному выше. Оно имеет вид

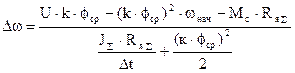
Расчет переходного процесса при усилении f производится аналогично, только кривая j=f(t) будет выглядеть так, как изображена на следующем рис.